码丁实验室,一站式儿童编程学习产品,寻地方代理合作共赢,微信联系:leon121393608。
人工智能(AI-Artificial Intelligence)是现在的科技领域最热门的一个词。作为计算机行业工作者,我们也会经常会被人问到底什么是人工智能,人工智能到底是怎么实现的等等问题。今天我们就来讲解一个相对简单、容易掌握、但很有效的人工智能算法,并用python来实现该算法让它识别图片里的数字。希望大家能在这个例子里知道一些人工智能的基本概念。
我们就直入主题,先说清楚今天的目标:下面是一些不同的数字图片,我们希望编一个python程序可以从这些图片里识别出它们分别是什么数字

这种任务是人工智能领域一个重要且常用的类别–图像识别。大家日常生活中也经常能接触到图像识别的技术,比如人脸识别、车牌识别等等。相信不用我再多介绍其作用和例子了。我们今天学习的是用K近邻算法来识别图片里数字。
关于K近邻算法,我们先用一个更简单的例子来说明:
西瓜还是哈密瓜
下面这个物体是西瓜还是哈密瓜呢?

我们大脑的思维过程大概是这样的:过往的经验告诉我们,西瓜一般比哈密瓜大,西瓜的表皮颜色是绿色的,而哈密瓜一般是黄色的。这个水果又大又绿,比较像我们经常见到的西瓜,所以应该是西瓜而不是哈密瓜。
细分的步骤如下:
在做出判断以前,我们的脑子里首先构建一个根据过往经验得出的图表(X代表西瓜;H代表哈密瓜):
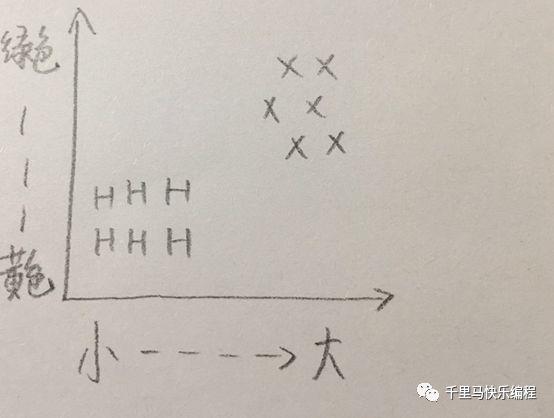
现在要判断一个新物体,它的大小和颜色介于西瓜和哈密瓜之间,像下面图表里问号所示的位置,那如何判断它是西瓜还是哈密瓜呢?
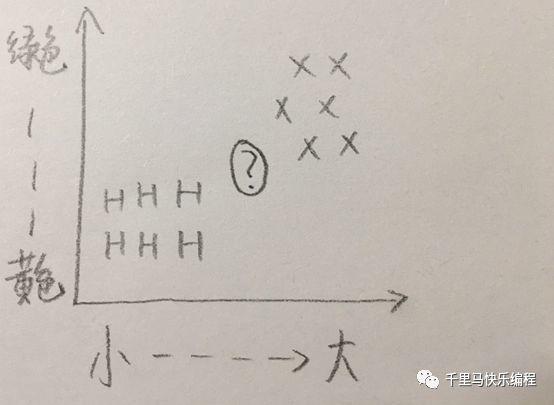
一种办法是看它的邻居,在特征图表里它最接近的三个邻居有两个是西瓜,一个是哈密瓜,西瓜近邻比哈密瓜多,因此这个水果更可能是西瓜。
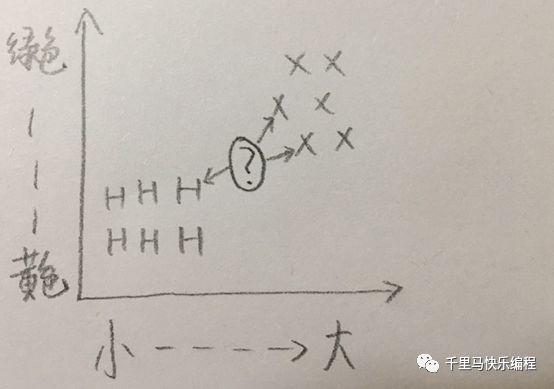
这种判断方法就是K近邻算法(k-nearest neighbors,下文我们用缩写knn表示),是不是非常简单?但它也是非常管用的。很多涉及分类的问题都可以用这种方法解决。
人工智能系统要处理各种各样的数据:图像、声音、文字等。分类是人工智能研究的一个重要的领域,它是要根据所给定数据的不同特点,判断它属于哪个类别的过程。
回到西瓜哈密瓜分类的问题,我们希望构建一个简单的人工智能系统,能够像人一样区分西瓜和哈密瓜,这种系统就叫做分类器。分类器必须根据要分类的事物特征进行工作,所以构造分类器系统第一步是要提取特征:
1.提取特征
西瓜哈密瓜的例子里,特征有两个:大小和表皮颜色。为了能够计算,我们需要把特征数字化。比如下面这个例子(已知A是哈密瓜,C是西瓜,问B是什么)的特征数字化后如图所示:

2. 特征空间
我们可以根据特征值在坐标系上绘图,一个点就代表了物体的一个特征,称为特征点。特征点构成的空间称为特征空间。在有两个特征值的情况下,绘出来的图是二维的:
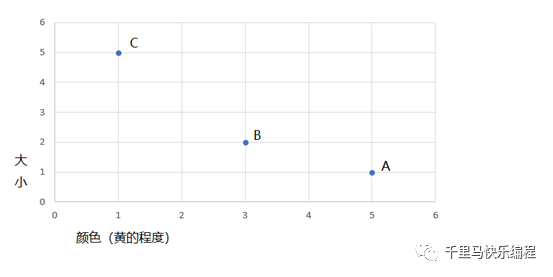
3. 距离计算
从上图我们看到B距离A比C近,但是到底有多近?把上图看成直角坐标系,A,B,C的坐标点分别用
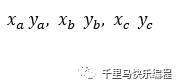
表示。
再用勾股定理我们可以很容易计算出
AB距离 =
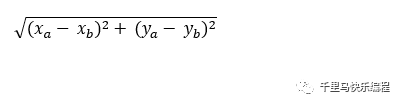
=2.24
BC距离 =
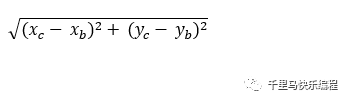
= 2.83
所以A和B比较近(像),更大的可能是哈密瓜。Knn的核心思想就是这么简单。
多维特征空间
如果特征多于两个怎么办呢?假设现在我们加上一个果肉颜色的特征:

那么它们的特征空间就是一个三维坐标空间了,它们的特征点位置分别如下图所示(三维图用Python的matplotlib库生成,红点代表A,绿点代表B,黄点代表C):
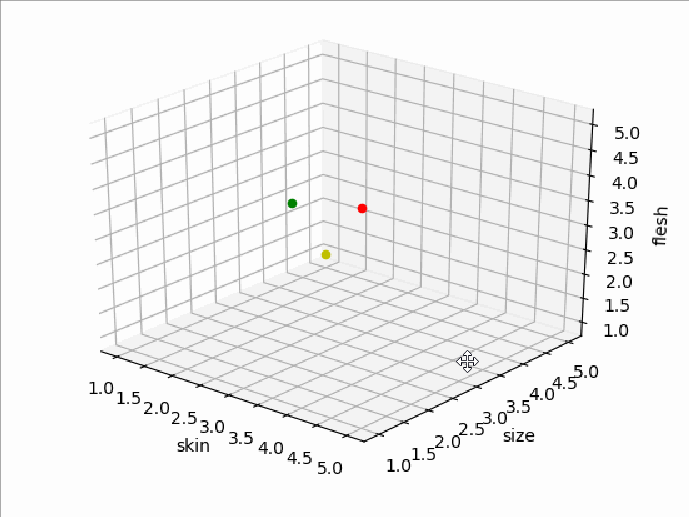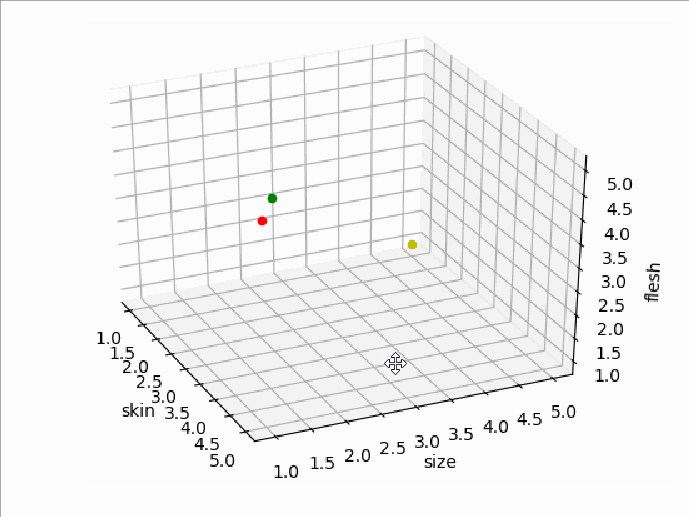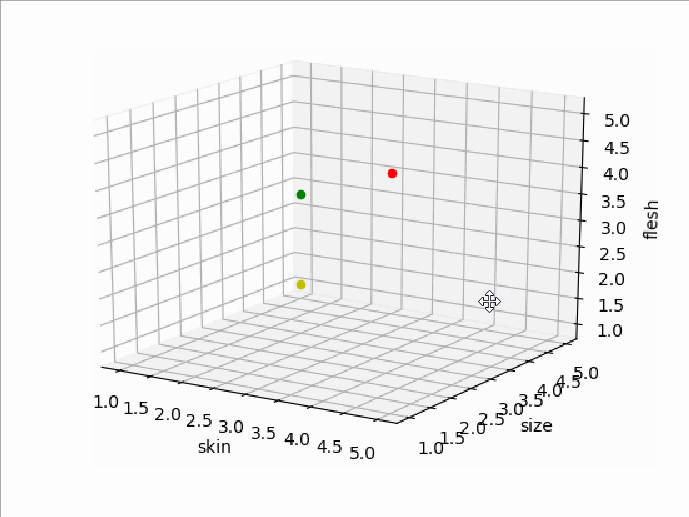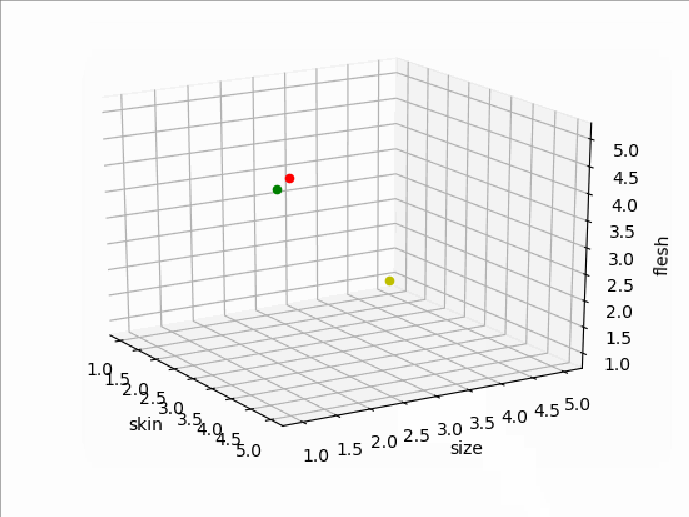
多维空间里两点间的距离叫做欧几里德距离。任意维数的空间里,如果将两个点的坐标分别标记为(p1,p2,p3….pn)和(q1,q2,q3…..qn),则欧几里德距离的计算公式为:

所以无论有多少个特征值,我们都可以通过上面的公式计算它们的距离,然后用Knn算法分类。
Knn的k
Knn的k表示用于选择最近邻居用来参照的数目。一般是奇数如1、2、3…,一般选3就可以了。
好了knn算法的原理就介绍完了。接下来我们就看看怎么用它来实现数字图片识别。
图像特征
图像识别的特征提取方法是一个比较复杂的话题,今天就不展开来讨论。我们使用的方法是把任意一个独立数字的图片转换成32*32像素的图片。每个点就代表一个特征值,所以特征空间是1024(32*32)维的。每个像素点的取值是0或者1。1代表该像素点是黑的(有内容的),0代表该点是空白的。下面有两个例子分别代表数字8、9:
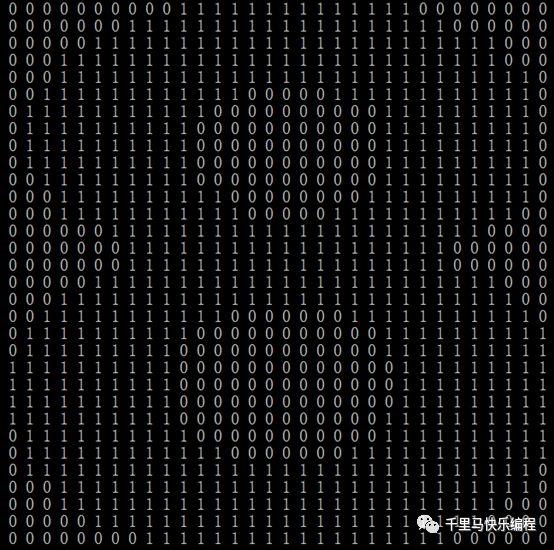
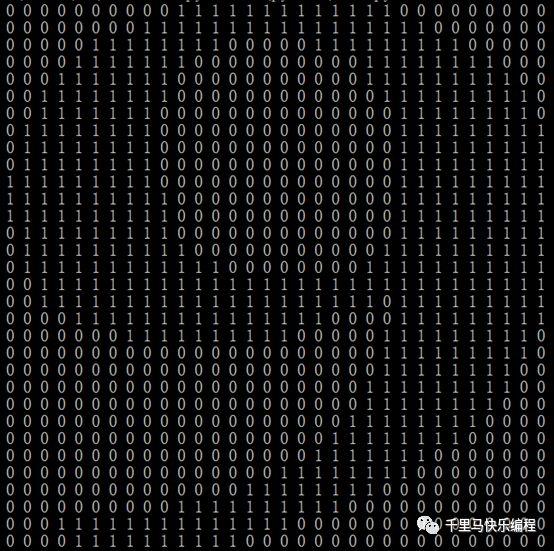
对于任何一个需要判断的数字图片,我们用同样的方法把它转换成上面的特征值,然后就可以用欧几里得距离公式计算1024维空间的距离了。
这种方法计算的欧几里得距离实际上是比较两个图片像素点的重合度,重合的像素越多,则我们认为它们越相似,这是一种简单直接而有效的图像特征比较方法。
图像预处理
我们还需要知道一些图像处理的基本知识:每个图片其实都是由n*m个像素点排列成一个n*m的长方形组成的。彩色图片的每个像素点都有一组代表R(红)、G(绿)、B(蓝)值的数据表示该像素点的颜色。它们的取值范围都在0-255之间。(R=0 G=0 B=0)代表纯黑色,(R=255 G=255 B=255)代表纯白色,(R=255 G=0 B=0)代表纯红色。
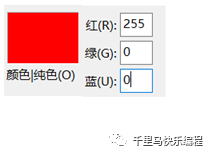
但是我们的数字识别需要的图片只要黑白就可以了,数字的颜色对于我们的识别没有什么意义。所以我们可以先把图像转换成灰阶模式(黑白照片模式)以减少数据量。灰阶模式图片没有颜色,只有灰度变化,每个像素只有一个灰度值,0代表全黑,255代表全白。下面第一个图是彩色RGB模式,第二个图是转换成灰阶模式后的效果:


接下来把灰阶图片简化,只要灰度值<128 (0 – 255的中间值),我们就用1表示该像素有内容;灰度值>=128就用0表示该像素有没有内容。这样就可以把图片转换成二进制特征空间了。上面数字“8”的灰阶图片简化后的二进制特征空间如下所示(它有50*49个像素点):

每个数字图片的大小不一样,边缘空白部分(数值为0)的大小也不一样。为了在平等的条件下对比,我们应该把图像边缘空白部分先裁剪掉,然后把图像转换成标准大小:我们这里选择32*32像素。
裁剪的方法是从第一行开始检查,如果该行全部都是数字0,则裁掉,直到找到一行有数字1的,把它设定为开始行;再从最后一行往上检查,如果该行全部都是数字0,则裁掉,直到找到一行有数字1的,把它设定为结束行。开始列和结束列也是用同样方法寻找。裁掉的是下图红色方框的部分:
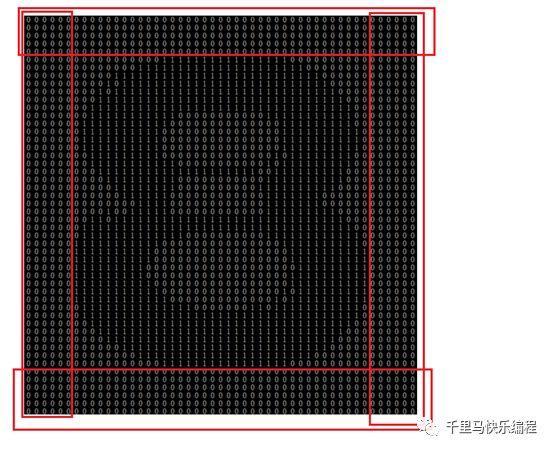
裁掉空白部分后,再把图片扩大或缩小到32*32像素,最后得出的二进制特征空间如下所示:
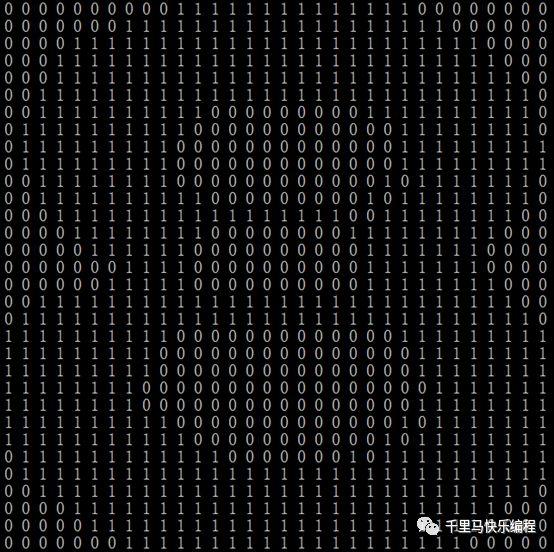
对于所有数字图片都作同样的处理,我们就能得到同样规格的没有边缘空白部分的图片数据,用来做“公平”的对比了。
收集数据、特征训练和分类
当代的人工智能普遍使用学习来获得进行预测和判断的能力。这样的方法被称为机器学习,它是人工智能的主流方法。机器学习通常从已知数据中去学习数据蕴含的规律或判定规则。但是,已知数据主要是用作学习的素材,而学习的主要目的是推广,也就是把学到的规则用来对新数据进行判断或预测。
Knn也需要收集已分好类的数据,用来和待分类的数据进行距离计算。但是knn的已知数据集并不是用来做标准意义上的训练,而是用来做对比,就是分类的过程。每一次对一个新数据进行分类,都需要把新数据和每一组已知数据进行距离计算,来查看新数据和已知数据的相似度。所以已知数据集越大越完整,能找到和新数据特征相似的几率越高,算法准确度就越高,但计算量也越大。这是一个需要平衡的问题。
在西瓜、哈密瓜的例子里,已知的水果A、C就是已知数据集,B是待分类的数据。在数字图片识别分类器里,我们也要事前准备好一系列已经分好类的数字图片作为已知数据集。下面是我们的已知数据集,它们的文件名就代表了分类:

我们的已知数据集每个数字(0-9)的已分类数据(图片)有6个。所以每一次对新数据(图片)进行分类都需要把新数据和6*10=60组已知数据进行距离运算。在现实生活中这个样本数量其实是非常小的,这么小的已知数据集必然导致算法准确度的降低,这一点必须要清楚。
分类错误率
我们用一个简单的标准来计算衡量分类器的效果:
分类错误率 = 分类错误的次数 / 分类次数
错误率越高,则该分类器效果越差。
Python的numpy库和PIL库
现在我们把用knn来区分数字图片的所有原理都弄明白了。在正式开始编程之前容我再简单介绍一下我们今天需要用到的两个python库:
- numpy库 : 主要是用来做矩阵(二维数组)的运算,这个库不是必需的。你可以直接使用python自带的数组。但numpy可以极大方便数组的处理,有了它我们可以用简单的几行代码算出欧几里得距离。推荐大家学习,对于日后的数据处理也是非常有用的。
- PIL库:用来处理图像,这是必需的库(当然有其他可代替的图片处理库)。
以下是涉及两个库的一些函数的解析:
ima = PIL.Image.open(file) #打开一个图片
ima = ima.convert(‘L’) #把图片转换成灰阶模式
im = numpy.array(ima) #把像素点保存到一个二维数组里
im.shape[0] #返回二维数组的行的数目
im.shape[1] #返回二维数组的列的数目
box =(startingCol,startingRow,endCol,endRow)
ima.crop(box) #把图片按box切割,startingCol,startingRow,endCol,endRow分别代表起始和结束位置
ima.resize((32,32)) #把图片等比例扩大或缩小成32X32像素
tileInput = numpy.tile(inputPoint,(dataSetSize,1)) #将inputPoint数组拓展,每一行的值都是inputPoint
diffMat = tileInput – dataSet #两个数组的差值
sqDiffMat = diffMat ** 2 #差值矩阵平方
sqDistances = sqDiffMat.sum(axis=1) #计算每一行上元素的和
distances = sqDistances ** 0.5 #开方得到欧几里得距离矩阵
sortedDistIndicies =distances.argsort() #按distances中元素进行升序排序后得到的对应下标的列表
Python程序代码
下面就是完整代码:
#-*- coding: utf-8 -*- import numpy import operator import time from os import listdir import PIL.Image '''图片预处理函数 ''' def pretreatment(file): ima = PIL.Image.open(file)#打开图片 ima = ima.convert('L') #把图片转换成灰阶模式 im = numpy.array(ima) #把像素点保存到一个二维数组 #set_printoptions(threshold=100000) '''下面开始把图片的开始和结束的空白部分去掉 ''' startingRow = 0 #去掉空白部分后的开始行 startingCol = 0 #去掉空白部分后的开始列 for startingRow in range(0,im.shape[0]): #从第一行开始循环,直到找到非空白行 if any(im[startingRow,:]<128): #非空白行的条件是至少有一个像素点灰阶<128 (256/2),灰阶0=全黑,255=全白,128代表黑和白的中间点。 break; for startingCol in range(0,im.shape[1]):#用同样的方法找到第一个非空白列 #print(j,im[:,j]) if any(im[:,startingCol]<128): break; endRow=im.shape[0]-1 #去掉空白部分后的结束行,从最后一行开始找 endCol=im.shape[1]-1 #去掉空白部分后的结束列,从最后一列开始找 while(endRow>-1): if any(im[endRow,:]<128): #非空白行的条件是至少有一个像素点灰阶<128 (256/2),灰阶0=全黑,255=全白,128代表黑和白的中间点。 break; else: endRow = endRow-1 while(endCol>-1): if any(im[:,endCol]<128): break; else: endCol=endCol-1 box = (startingCol,startingRow,endCol,endRow) #切割图片,把开始部分和结束部分的空白行/列切掉,切割完后 newima = ima.crop(box).resize((32,32))#把切割后图片等比例转换成32*32像素图片 names = file.split('/') newima.save("c:/python/temp/"+names[len(names)-1]) #保存一个临时文件以用来检查处理后的图片是否正确 im = numpy.array(newima) #重新用二维数组保存图片像素 returnV =[] # 最终函数返回值是一个1024(32*32)位的一维数组,就是把图片像素按行展开来。每个元素值是0或1。 for i in im: for x in i: f = lambda x:1 if x<128 else 0 #灰阶转换成0/1值 - 灰阶<128 (256/2) 为1。灰阶0=全黑,255=全白,128代表黑和白的中间点。 returnV.append(f(x)) return returnV '''分类函数 inputPoint - 代表待分类图片的1024位一维数组 dataSet - 代表训练集的二维数组 labels - 已分好的类别 k - knn算法的k ''' def classify(inputPoint,dataSet,labels,k): dataSetSize = dataSet.shape[0] #已知分类的数据集(训练集)的行数 tileInput = numpy.tile(inputPoint,(dataSetSize,1)) #将输入点拓展成与训练集相同维数的数组,就是把就是把一维数组扩展成二维,每一行的值都是inputPoint diffMat = tileInput - dataSet #样本与训练集的差值矩阵 sqDiffMat = diffMat ** 2 #差值矩阵平方 sqDistances = sqDiffMat.sum(axis=1) #计算每一行上元素的和 distances = sqDistances ** 0.5 #开方得到欧拉距离矩阵 sortedDistIndicies = distances.argsort() #按distances中元素进行升序排序后得到的对应下标的列表 #选择距离最小的k个点 classCount = {} for i in range(k): voteIlabel = labels[ sortedDistIndicies[i] ] classCount[voteIlabel] = classCount.get(voteIlabel,0)+1 #按classCount字典的第2个元素(即类别出现的次数)从大到小排序 sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse = True) return sortedClassCount[0][0] '''从文件名中解析分类数字 规则是0-1.png,0代表数字分类,1代表第1个样本 ''' def classnumCut1(fileName): fileStr = fileName.split('.')[0] classNumStr = int(fileStr.split('-')[0]) return classNumStr #构建训练集数据向量,及对应分类标签向量 def trainingDataSet(): t1 = time.time() hwLabels = [] #用来输出分类列表 trainingFileList = listdir('c:/python/test') #从这个目录里读取已分好类的训练图片 m = len(trainingFileList) trainingMat = numpy.zeros((m,1024)) #m*1024个数据的训练集,每个元素初始化为0 for i in range(m): fileNameStr = trainingFileList[i] hwLabels.append(classnumCut1(fileNameStr))#hwLabels记录了每个文件代表的数字分类 trainingMat[i,:] = pretreatment('c:/python/test/%s' % fileNameStr)#trainingMat的每一行保存了0/1代表的处理后的一张图片 t2 = time.time() print("Training time: %.2fmin, %.4fs."%((t2-t1)//60,(t2-t1)%60)) #训练耗时 return hwLabels,trainingMat #返回分类列表 及训练集特征数组 #测试函数 def test(): hwLabels,trainingMat = trainingDataSet() #构建训练集 testFileList = listdir('c:/python/tt') #从这个目录里读取要测试的图片 errorCount = 0.0 #用来记录错误的次数 mTest = len(testFileList) #用来记录测试的次数 t1 = time.time() #用来记录测试时间 for i in range(mTest): fileNameStr = testFileList[i] classNumStr = classnumCut1(fileNameStr) #测试集也是预先分好类的 vectorUnderTest = pretreatment('c:/python/tt/%s' % fileNameStr) #预处理图片 classifierResult = classify(vectorUnderTest, trainingMat, hwLabels, 3)#调用knn算法进行分类 #打印分类结果 print("the test result is: %d, the actual number is: %d %s" % (classifierResult, classNumStr, classifierResult==classNumStr)) if (classifierResult != classNumStr): errorCount += 1.0 #记录错误 print("nthe total number of tests is: %d" % mTest) #输出测试总样本数 print("the total number of errors is: %d" % errorCount) #输出测试错误样本数 print("the total error rate is: %f" % (errorCount/float(mTest))) #输出错误率 t2 = time.time() print("Test time: %.2fmin, %.4fs."%((t2-t1)//60,(t2-t1)%60)) #测试耗时 test()#主函数
运行结果
我们测试了本文开始时提到的13个图片,结果如下:
Training time: 0.00min, 0.5724s.
the test result is: 0, the actual number is: 0 True
the test result is: 1, the actual number is: 1 True
the test result is: 1, the actual number is: 1 True
the test result is: 2, the actual number is: 2 True
the test result is: 2, the actual number is: 2 True
the test result is: 2, the actual number is: 2 True
the test result is: 3, the actual number is: 3 True
the test result is: 5, the actual number is: 5 True
the test result is: 8, the actual number is: 5 False
the test result is: 6, the actual number is: 6 True
the test result is: 7, the actual number is: 7 True
the test result is: 8, the actual number is: 8 True
the test result is: 9, the actual number is: 9 True
the total number of tests is: 13
the total number of errors is: 1
the total error rate is: 0.076923
Test time: 0.00min, 0.3476s.
错误率是7%。但因为训练集(已知数据集)和测试数据量都太小,这个错误率的真实性不高。大家有时间可以扩大数据量来看看实际效果如何。程序还输出了运行时间。大家可以在扩大数据量的测试时观察一下数据量和运行时间的关系。
我们的简单训练集和测试集图片可以在这里下载:http://qianlima.love:8001/knn/
Knn的优缺点
优点
简单,易于理解,易于实现,无需估计参数,无需训练。
适合对稀有事件进行分类(例如当流失率很低时,比如低于0.5%,构造流失预测模型)。
特别适合于多分类问题 (对象具有多个类别标签),例如根据基因特征来判断其功能分类,knn比支持向量机的表现要好。
缺点
性能低:大家应该都能看到knn用来做图像识别的执行效率并不高,因为每个测试数据都要和所有已知数据进行距离计算,每个距离计算包括了1024个维度浮点运算,此外,我们还要为已知数据集和测试数据准备大量内存。
解释性差: Knn的另一个缺陷是它无法给出任何数据的基础结构信息或数据特征规则,比如8和6到底有什么不同。
小结
但愿大家能通过本文的学习,对knn和机器学习的基本知识和用途能有大致的认识。机器学习是人工智能的重点研究方向,同时也是很有趣的一个领域,希望大家下定决心,学好数学、学好编程,以后在该领域取得成果和快乐。

