11月10日，北京大学李晓明教授在浙江省江山中学上了一堂精彩的高中信息技术新课标的试验课，其课堂巩固环节的作业题如下：
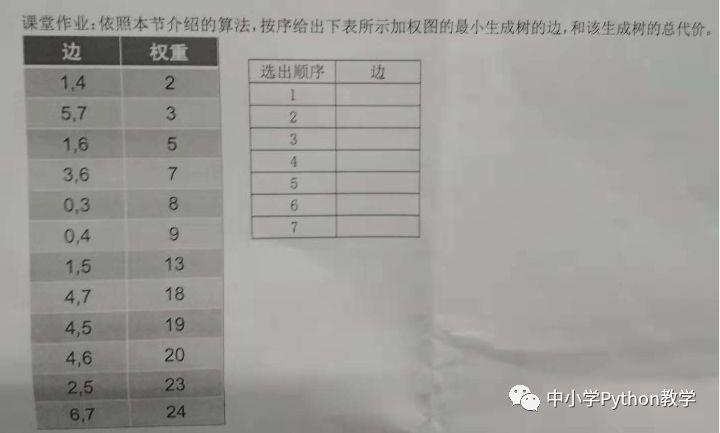比较普通的算法是用普里姆算法实现，普里姆算法是一种构造最小生成树的算法，其基本思想：按逐个顶点将顶点连通的方式来构造最小生成树。
python heapq是一个最小堆，堆顶元素为最小值，最小（大）堆的逻辑结构是一颗二叉树，其中父节点小（大于）于左右子节点，物理结构为一个数组。 heapq模块支持heappush（入堆）、heappop（出堆）、heapify（创建堆）等操作，详细请参考python官方文档
（https://docs.python.org/2/library/heapq.html）。
上述作业题的python参考代码如下：
from collections import defaultdict
from heapq import heappush,heappop,heapify
def Prim(nodes, edges):
#基于最小堆实现的Prim算法
element = defaultdict(list)
for start, stop, weight in edges:
element[start].append((weight, start, stop))
element[stop].append((weight, stop, start))
all_nodes = set(nodes)
used_nodes = set(nodes[0])
usable_edges = element[nodes[0]][:]
heapify(usableedges)
# 建立最小堆
MST = []
while usableedges and (allnodes – usednodes):
weight, start, stop = heappop(usableedges)
if stop not in usednodes:
usednodes.add(stop)
MST.append((start, stop, weight))
for member in element[stop]:
if member[2] not in usednodes:
heappush(usableedges, member)
MST=sorted(MST,key=lambda MST: MST[2])
return MST
def main():
nodes = list(’01234567′) #节点
#原始加权图表
edges = [("1", "4", 2), ("5", "7", 3),
("1", "6", 5), ("3", "6", 7),
("0", "3", 8), ("0", "4", 9),
("1", "5", 13), ("4", "7",18),
("4", "5", 19), ("4", "6", 20),
("2", "5", 23), ("6", "7", 24),
]
print(“n原始加权图表为 :”, edges)
print(“n最小生成数的边为 : “)
print(Prim(nodes, edges))
if name == ‘main‘:
main()
运行结果如下：
