友情提示：380元/半年，儿童学编程，就上码丁实验室。
有个非常棒的爱写代码的十岁小朋友的公众号发了这个问题，她的思路是正确的，但是代码逻辑有点问题，最终个数是对的，但是细看序号，则是错误的。；)。
于是我自告奋勇来把这个问题重解一下。问题是这样的：
解题思路：
把1-100名同学的这个初始范围作为下面图形的灰色方框内的范围，其中2、3、5的倍数分别用三个圆形表示。如果一个数字同时是2、3的倍数，那么它的范围就是2、3圆形的交集。如果一个数字同时是2、3、5的倍数，那么它的范围就是2、3、5圆形的交集。
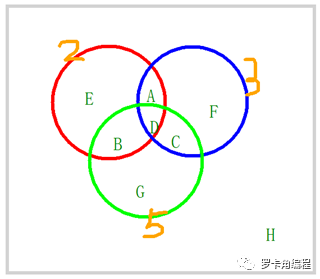
这个解题思路，借鉴的是文氏图方法。
这道题的数学解法思路为：100以内的是2、3、5的倍数的数字个数是100//(2*3*5)=3，也即100整除2×3×5的乘积30，结果为3.也即图形的D区域代表的个数为3.
以此类推：
D=3
A=100//(2*3)-D=16-3=13
B=100//(2*5)-D=10-3=7
C=100//(3*5)-D=6-3=3
E=100//2-(A+B+D)=50-(13+7+3)=27
F=100/3-(A+D+C)=33-(13+3+3)=14
G=100/5-(B+D+C)=20-(7+3+3)=7
H=100-(A+B+C+D+E+F+G)=100-(13+7+3+3+27+14+7)=26
按题目的说明，最终面向老师的同学序号，应该是一次也没向后转的H，再加上两次向后转的（A+B+C），那么最终的面向老师的个数为H+(A+B+C)=26+(13+7+3)=49。
而背向老师的同学序号，应该是转了一次的E、F、G，再加上后转三次的D，总和为51。
下面使用Python语言，来解上面的问题。
第一种解法，根据上面的算法，类似于计算H+(A+B+C)的个数：
def f(n):
if (n % 2 == 0 and n % 3 == 0 and n % 5 == 0):
return False
return True
l = []
for i in range(1, 101):
if not (i % 2 == 0 or i % 3 == 0or i % 5 == 0) or f(i) and ((i % 2 == 0 and i % 3 == 0) or (i % 2 == 0 and i %5 == 0) or (i % 3 == 0 and i % 5 == 0)):
l.append(i)
print(l)
print(len(l))
第二种解法，逻辑上更为简洁。也即判断每个数字的后转次数，最终面向老师的同学，是后转次数为0，和后转次数为2的同学。
def f(n):
if (n % 2 == 0 and n % 3 == 0 and n % 5 == 0):
return 3
elif (n % 2 == 0 and n % 3 == 0) or (n % 2 == 0 and n % 5 == 0) or (n %3 == 0 and n % 5 == 0):
return 2
elif (n % 2 == 0 or n % 3 == 0 or n % 5 == 0):
return 1
else:
return 0
l = []
for i in range(1, 101):
if (f(i) ==0 or f(i) ==2):
l.append(i)
print(l)
print(len(l))
这两种方法得出的答案一致，均为49个。序号为:
[1, 6, 7, 10, 11, 12, 13, 15, 17, 18, 19,20, 23, 24, 29, 31, 36, 37, 40, 41, 42, 43, 45, 47, 48, 49, 50, 53, 54, 59, 61,66, 67, 70, 71, 72, 73, 75, 77, 78, 79, 80, 83, 84, 89, 91, 96, 97, 100]
附录：
文氏图（英语：Venn diagram），或译Venn图、 [1] 温氏图、维恩图、范氏图，是在所谓的集合论（或者类的理论）数学分支中，在不太严格的意义下用以表示集合（或类）的一种草图。它们用于展示在不同的事物群组（集合）之间的数学或逻辑联系，尤其适合用来表示集合（或）类之间的“大致关系”，它也常常被用来帮助推导（或理解推导过程）关于集合运算（或类运算）的一些规律。
