Scratch角度体系 PK 数学角度体系!

Scratch中的方向是一个很重要的内容，大家可以使用方向，很容易地让角色面向一个方向或向一个方向移动。

但大家是否注意到了，Scratch中使用的方向体系与在数学中学习到的方向体系不是一样的呢？如果用来进行数学绘图等工作，就会遇到问题。

今天，我们就在这里论述一下这个问题，研究一下他们之间的关系，更重要的是如何在两个体系之间进行换算。

我们首先看一下SCRATCH中的角度体系是什么样的？

 

从方向积木的下拉框中可以看到，

0度表示向上，

90度表示向右，

－90度表示向左，

180度表示向下。

大家都知道一周是360度，我们可以使用下图表示Scratch中角度与方向的对应关系。

 

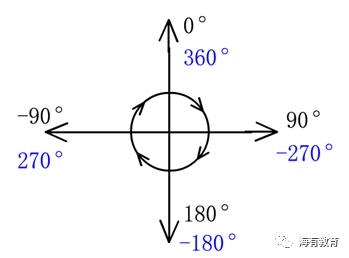
可以看出，角度是沿顺时针方向增加的。

每个方向上角度的两种表示方式（实际上还可以再增加或减小360度的整数倍），表示的方向是相同的。

 

这个角度体系实际上类似于钟表中时针的角度体系，从0度0点开始，顺时针转动，90度对应3点，180度对应6点，270度对应9点。

下面，我们再来看看数学中的角度体系。

如果大家学习了数学中的象限及三角函数，就会知道，在数学中角度的定义是不同的。

图中展示了数学中的角度定义。

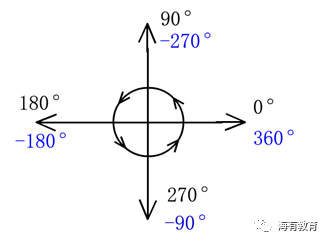
可以看到向右是0度，向上是90度，向左是180度，向下是270度。

角度是按逆时针方向增加的。

当然，也存在增加或减小360度整数倍的等价角度。

 

 通过几个图的对比，会发现，Scratch中的方向和数学中的方向不一样。

 

所以问题就来了，在有些程序中，我们要同时使用Scratch中的方向和数学中的方向。例如我们要做这样一个程序：一个小球绕一个箭头转动，而箭头要一直面向小球。在这里箭头的旋转用的是Scratch中的方向，而小球的运动是用数学的计算坐标得到的。

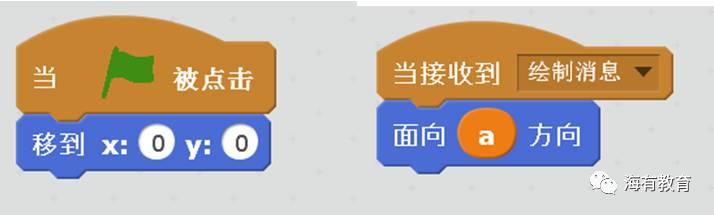
我们建立一个全局变量a 用于保存当前的角度。在舞台中对a进行初始化，并处理a的增加，每增加一次a发送绘制消息。

下面是箭头角色中的脚本：接收消息后，一直指向a方向。

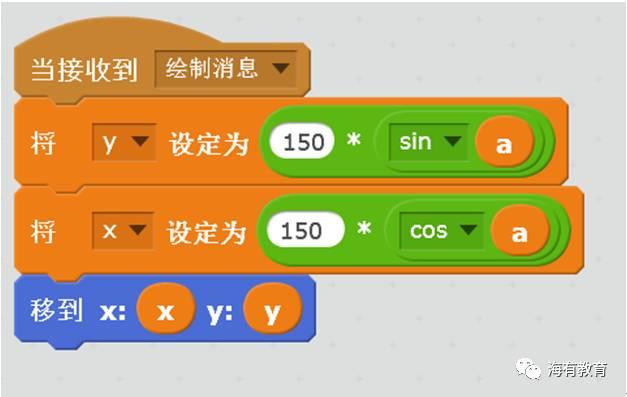
小球运动的坐标是标准的数学方式，通过y=r*sin(a), x=r*cos(a)计算坐标，并移动到坐标处。

运行后可以看到，由于角度体系的不同，两个角色在向不同的方向运动，南辕北辙了。

 

那么，如何解决这个问题呢？

我们列表分析一下：

方向	Scratch体系角度	数学体系角度	关系
向上	0	90	0+90=90
向右	90	0	90+0=90
向下	180	270(-90)	180+(-90)=90
向左	270	180(-180)	270+(-180)=90

可以看出：同一个方向时，两个体系的角度之和正好为90度。

所以我们可以得到两者的关系。

当知道一个体系的角度时，使用90度减去这个角度，就能够得到另一个体系中的角度了。

 

应用这个方法，我们改变一下上面的程序。

可以修改箭头程序或球的程序，我们修改一下箭头的方向。只需要修改成下面这样。将原来的指向a方向修改为指向90-a方向。就能达到我们的要求了。

再运行一下，可以看到，箭头会一直指向球体，达到了我们的要求。

 

怎么样，下次再涉及到方向和角度体系的问题，就可以用这样的方式进行处理了。当然，关于角度还有更多的需要掌握的知识，我们以后会逐步地进行讲解。

 

参考资料

1象限：

https://baike.baidu.com/item/%E8%B1%A1%E9%99%90

2象限角：

https://baike.baidu.com/item/%E8%B1%A1%E9%99%90%E8%A7%92

转自公众号：
海有教育