友情提示：380元/半年，儿童学编程，就上码丁实验室。
一个经典的智力问题：有一只小猫爱喝酒，一天，听说酒店买酒有优惠：一瓶酒两元钱。2个空酒瓶或4个瓶盖可换1瓶啤酒。小猫一次可以喝10瓶酒，心想今天拿10元钱去喝酒，肯定不会醉。小猫按照酒店的优惠信息，花了10元钱，把能兑的酒也都喝了。请问小猫喝醉了没？他到底一共喝了多少酒？
好吧，一些朋友可能已经算出来了。那么我增加难度：
过了一年，小猫苦练酒量，一次可以喝10000瓶酒了。这次，他拿了10000元去酒吧，结果酒吧又是相同的促销活动。于是，小猫按照同样的优惠信息，拿了10000元去喝酒，且全部喝完了。请问小猫喝醉了没？他到底一共喝了多少酒？
要知道，这个时候，如果不借助公式或工具，再计算是相当困难的。
我们回到10元钱喝酒的问题。每获得一瓶酒，可以有三种方式：1.花2块钱买；2. 用2酒瓶换；3. 用4瓶盖换
将每获得一瓶酒并喝掉它视为一个步骤，整个消费过程由有限有序步骤组成，每一步有三种执行方式。考察任一步骤前后“酒瓶和瓶盖的总个数（记为N）”的变化。
很容易得到：若该步采取方式1，则N+2；若该步采取方式2，则N不变；若该步采取方式3，则N-2。
考虑初态（即第一步之前）：N=0。因此，每一步之后N总是偶数。
考虑末态（即最后一步之后）。末态当然是消费者钱和酒瓶和瓶盖都不够，再也搞不到酒的时候呗。
钱不能增加，所以末态金钱0；最后一步喝了一瓶酒，所以末态至少有1个瓶盖和1个酒瓶。
不仅如此，由于每一步都喝了一瓶酒，所以每一步之后都至少有1瓶盖和1酒瓶。
因此末态时N≥2且N为偶数。
1. N≥6时，瓶盖数≥4和酒瓶数≥2必有至少一个成立，这显然不是末态。
2. N=2时，瓶盖数=酒瓶数=1。若最后一步采用方式1，那之前N=0（总步骤数显然大于1），矛盾；若最后一步采用方式2，则之前瓶盖数为0，矛盾；若最后一步采用方式3，则之前酒瓶数为0，矛盾。总而言之N=2不可能是末态。
于是末态的时候只能有N=4；符合末态条件的N=4只有1酒瓶+3瓶盖。附：金钱0。
接下来有了理论支持就可以暴力求解最大值了。设一瓶酒里的酒价值x，酒瓶价值y，瓶盖价值z，随手列个三元一次方程组解得：
x=1/2，y=1，z=1/2 （单位元）
于是：初态猫有10元，末态猫有2.5元。整个消费过程是等价交换，消失的那些钱去哪儿了？变成酒进猫肚儿了呗。
7.5÷1/2=15。
当然，使用这个方式倒是可以计算出10000元喝多少酒。
但是，我们用工具就简单多了。
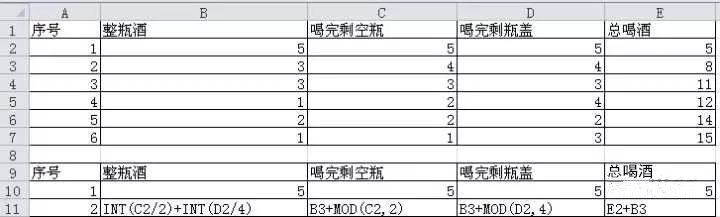
例如，如果我们用excel，可以这样：
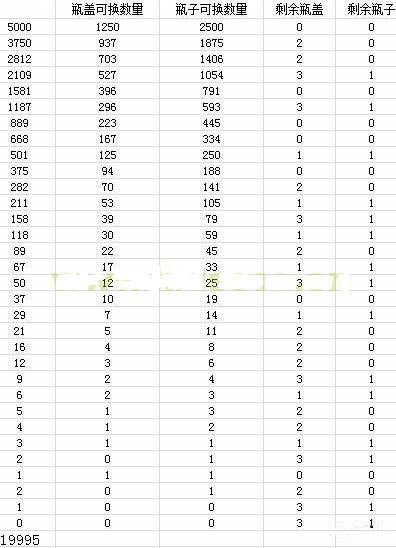
那么，我们会Scratch编程的朋友，能不能想到如何使用Scratch来计算呢？这里给出了答案：
作品链接: https://pan.baidu.com/s/1hrDlFl6 密码: fpd9
事实上，我们用Scratch还可以解决很多数学智力问题。所以Scratch会是我们的好朋友。你看，用这个智力题做了一个简单的故事，趣味性更强了。