友情提示：380元/半年，儿童学编程，就上码丁实验室。
【汉诺塔】法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说：在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。
后来，这个传说演变成了汉诺塔游戏。而这个游戏又成为人们学习递归算法的一个经典案例。
【游戏描述】有A、B、C三根相邻的柱子。A柱上有若干个大小不等的圆盘，大的在下，小的在上。要求把这些盘子从A柱移到C柱，中间可以借用B柱，但每次只许移动一个盘子，并且在移动过程中，3个柱子上的盘子始终保持大盘在下，小盘在上。
【计算移动步数】计算公式：n个圆盘的移动步数 = 2的n次方减1。
比如：1个圆盘时，2的1次方减1 = 1步；2个圆盘时，2的2次方减1 = 3步；3个圆盘时，2的3次方减1 = 7步；4个圆盘时，2的4次方减1 = 15步；5个圆盘时，2的5次方减1 = 31步；……
64个圆盘时，2的64次方减1 = ?
打开电脑中的“计算器”，算一下2的64次方，结果如图：
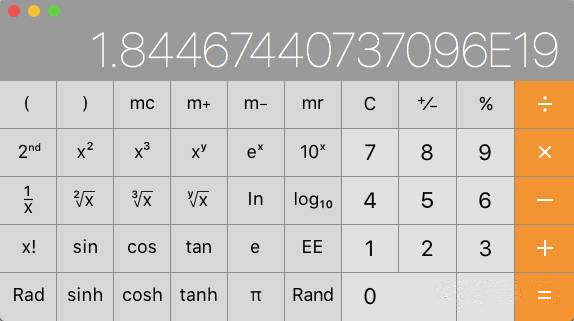
如果有64个盘子，大约要移动1800亿亿步。看清楚了，是“亿亿”。如果1秒钟移动1步，那么1年可以移动31,536,000步，即约3000多万步。这样把64个盘子移动完成，大约需要584,942,417,355年，即约5800多亿年。
据科学家推测，宇宙大约诞生在200多亿年前。回到传说中僧侣们的预言，用不了5800多亿年，也许我们的世界早就消失了。
【游戏解法】我们把游戏规则总结为3条：1、把全部圆盘从A柱移到C柱上；2、每次只能移动一个圆盘；3、小盘只能放在大盘上面。
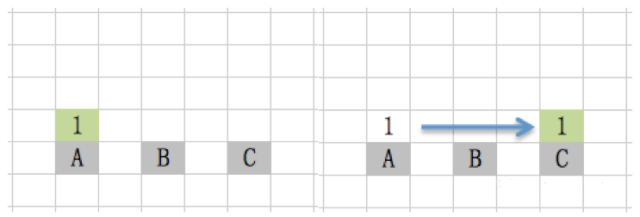
1个盘子的情况（n=1）
因为n-1=0，所以在有1个盘子时，直接把1号盘从A柱移到C柱。只需1步。
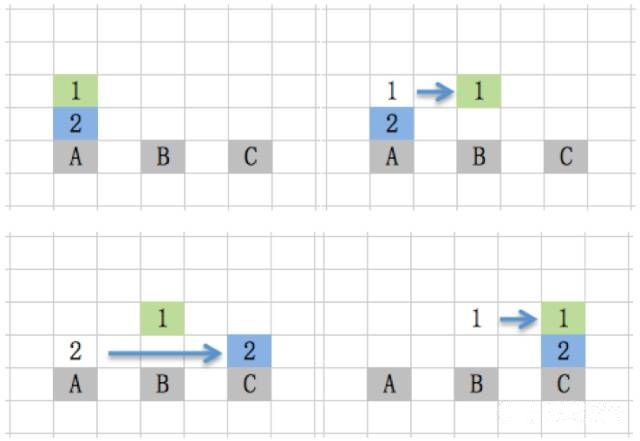
2个盘子的情况（n=2）
如果有2个盘子，先把1号（n-1=1）盘子移到B柱，再把2号（n=2）盘子移到C柱，最后把1号（n-1=1）盘从B柱移到C柱。共需要3步。
3个盘子的情况（n=3）
如果是2个以上的盘子，则问题就变得复杂了。
我们以3个盘子为例，分别用3种颜色表示不同盘子，并为3个盘子编号，1号盘最小，3号盘最大。3个盘子开始都放在A柱上。现在要把3个盘子都移到C柱上，该如何操作？
根据汉诺塔游戏规则，移动步骤为：
1、先把1~2号（n-1 = 2）盘以C柱为中转，都移到B柱上；
2、再把3号（n=3）盘从A柱移到C柱；
3、最后把B上的1~2号（n-1=2）盘以A为中转，都移到C柱上。
我们先来看第1个步骤。由于只移动1、2号盘，我们先把3号盘用阴影遮住。移动步骤：1号盘由A到C，2号盘由A到B，1号盘由C到B。
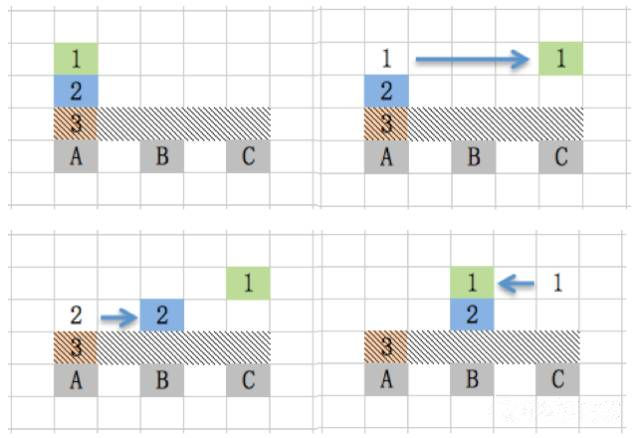
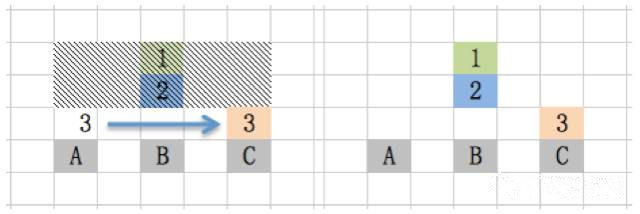
接着看第2个步骤。这时1、2号盘已经在B柱上，而C柱是空的，只要把3号盘直接从A柱移到C柱就可以了。
最后是第3个步骤。这时3号盘已经在C柱上了，只要移动1、2号盘。我们先把3号盘用阴影遮住。移动步骤：1号盘由B到A，2号盘由B到C，1号盘由A到C。
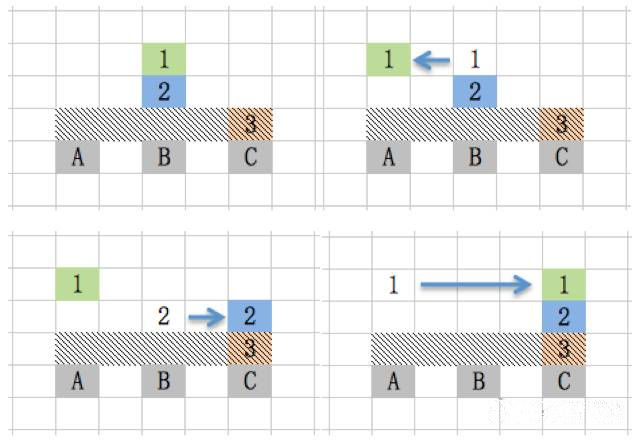
到这里，用了7步，就把3个盘子从A柱移到C柱。
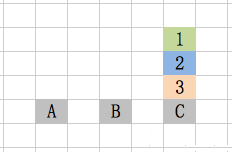
n个盘子的情况
把汉诺塔的移动步骤总结为：
1、先把1~n-1号盘由C柱中转，从A柱移到B柱上。
2、再把n号盘从A柱移到C柱；
3、最后把1~n-1号盘由A柱中转，从B柱移到C柱。
【问题】用Scratch编写一个汉诺塔程序，根据盘子数量，求出将全部盘子从A柱移到C柱的步骤。
【编程解题】汉诺塔的移动步骤讲解起来比较复杂，但是编写程序却是非常简单，因为我们使用递归算法。
所谓递归，就是程序调用自身的编程技巧。在Scratch中使用递归，我们可以在一个模块中调用该模块自身。比如在解决汉诺塔问题时，模块“移动盘子”就是一个采用了递归结构的程序。
下面我们开始编程解决汉诺塔问题。
创建一个名为“日志”的列表，用于记录汉诺塔的移动步骤。
创建一个名为“移动盘子”的模块，参数有4个：n、A、B、C，分别表示盘子数量、A柱名称、B柱名称、C柱名称。该模块采用的递归结构。移动盘子的步骤为：
1、调用“移动盘子”模块，把n-1个盘子以C柱为中转，从A柱移到B柱。
2、直接将n号盘从A柱移到C柱。这里用“日志”列表记录移动步骤。
3、调用“移动盘子”模块，把n-1个盘子以A柱为中转，从B柱移到C柱。
该模块使用递归结构。递归的结束条件是n=0。这里是n大于0时，才执行上述移动步骤。每一轮移动，都是先把上面的n-1个盘子移走，然后才能移动第n个盘子。在移动过程中，A、B、C三个柱子的角色会发生变换。
模块“移动盘子”的完整代码如下：
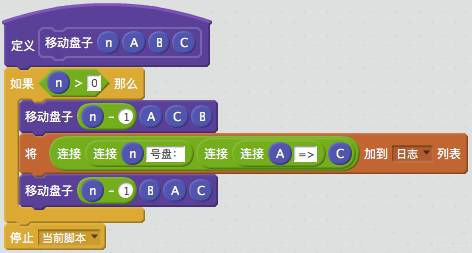
入口程序：
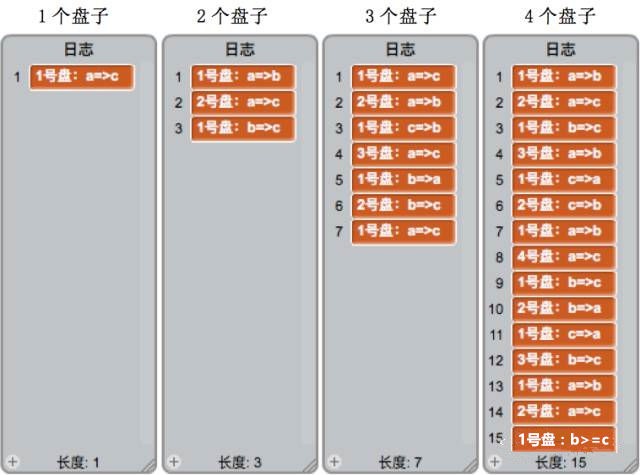
修改参数并运行程序，得到盘子数量分别为1、2、3、4时的移动步骤：
