码丁实验室,一站式儿童编程学习产品,寻地方代理合作共赢,微信联系:leon121393608。
《数学的故事》里面说了数学家笛卡尔的一个故事:
1649年, 斯德哥尔摩的街头,52岁的 笛卡尔邂逅了18岁的瑞典公主克里斯汀。几天后,他意外的接到通知,国王聘请他做小公主的数学老师。跟随前来通知的侍卫一起来到皇宫,他见到了在街头偶遇的女孩子。从此,他当上了小公主的数学老师。
小公主的数学在笛卡尔的悉心指导下突飞猛进,笛卡尔向她介绍了自己研究的新领域– 直角坐标系。每天形影不离的相处使他们彼此产生爱慕之心,公主的父亲国王知道了后勃然大怒,下令将笛卡尔处死,小公主克里斯汀苦苦哀求后,国王将其流放回法国,克里斯汀公主也被父亲软禁起来。
笛卡尔回法国后不久便染上重病,他日日给公主写信,因被国王拦截,克里斯汀一直没收到笛卡尔的信。笛卡尔在给克里斯汀寄出第十三封信后就气绝身亡了,这第十三封信内容只有短短的一个公式:r=a(1-sinθ)。国王看不懂,觉得他们俩之间并不是总是说情话的,将全城的数学家召集到皇宫,但没有一个人能解开,他不忍心看着心爱的女儿整日闷闷不乐,就把这封信交给一直闷闷不乐的克里斯汀。
公主看到后,立即明了恋人的意图,她马上着手把 方程的图形画出来,看到图形,她开心极了,她知道恋人仍然爱着她,原来方程的图形是一颗心的形状。这也就是著名的“心形线”。
国王死后,克里斯汀登基,立即派人在欧洲四处寻找心上人,无奈斯人已故,先她一步走了,徒留她孤零零在人间…

笛卡尔心形如上图所示是不是觉得不太像我们经常看到的心形?没关系,我们今天就来学习用Scratch画出更漂亮的心形图和其他的函数曲线。
函数曲线
在二维平面,如果有函数 f(x) = y,则该函数可以在平面直角坐标系上呈现为一条曲线。其中任意一组x,y值分别是该曲线上的点的横坐标和纵坐标值。
许多美丽的曲线图形都可以由简单的数学函数关系生成。在计算机没有普及的时候,绘制函数曲线是很复杂的工作。现在借助于Scratch等工具,我们可以很方便地画出各种优美的函数曲线图形,感受数学之美。
一次函数
若两个变量x,y间的关系式可以表示为y=kx+b(k,b为常数,k≠0)的形式,则称y是x的一次函数(x为自变量,y为因变量)。
我们先从最简单的一次函数y=x开始。x是横坐标,y是纵坐标。y=x函数的意思就是横坐标和纵坐标的值永远一样,即:
x=1 时 y=1
x=2 时 y=2
……
x=100 时 y=100
在Scratch里,我们就可以通过下面的方法通过画100个点,并把它们连起来画出y=x的函数曲线:
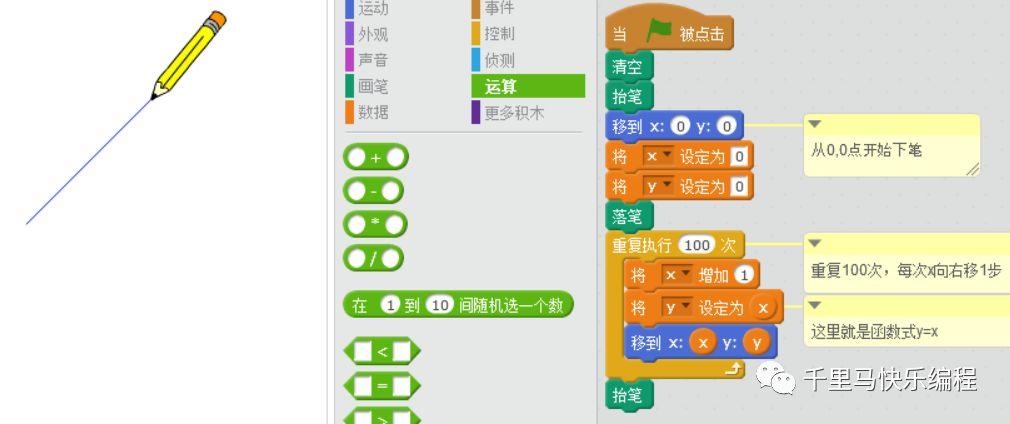
我们只需要增加两个变量k、b,并改变函数,就可以以画出任意一次函数y=kx+b的曲线。先不要急着画,我们先讨论一下编程里的“函数”概念,它其实和数学的函数是类似。
复习一下数学里“函数”的定义:给定一个数集A,假设其中的元素为x。现对A中的元素x施加对应法则f,记作f(x),得到另一数集B。假设B中的元素为y。则y与x之间的等量关系可以用y=f(x)表示。我们把这个关系式就叫函数关系式,简称函数。函数概念含有三个要素:定义域A、值域B和对应法则f。其中核心是对应法则f,它是函数关系的本质特征。
编程里的函数也有类似但不完全一样的概念,其中函数的输入参数可以看做是定义域A,函数的运行所改变的结果可以看做值域B,而函数的算法(过程)就是对应法则f。
Scratch里我们可以在“更多积木-制作新的积木”指令里建立新函数。下面我们来建立y=kx+b的函数:
1、自定义函数名–一次函数
2、添加三个数字输入参数k、b、x

3、定义函数体:把y设成等于k*x+b
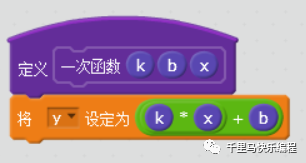
上面三步定义了一个简单的函数。这样做的一个最显而易见的好处是以后每次要计算y=k*x+b的时候,我们只需要拖动“一次函数”到相应的地方就可以了;要改变函数内部结构的时候,也是改变一次函数的定义部分就可以了。函数内部越复杂,就越能节省开发时间并避免重复开发的错误。
下面是完整的一次函数曲线的程序和效果图:
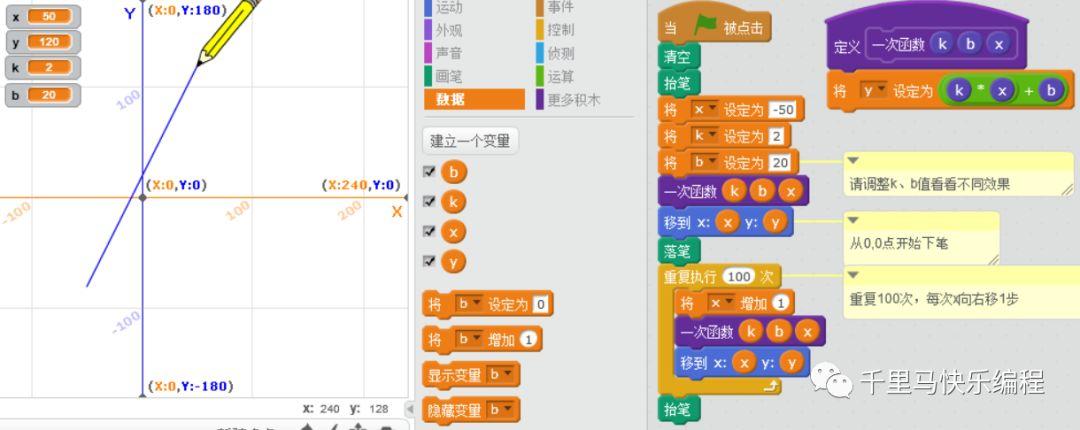
大家试着改变k、b值看看不同的效果吧。
上图的程序脚本部分中黄色的说明部分叫做“注释”,它一般是用来解释程序的某段脚本的作用或用法。它不会影响程序的执行。但是对于程序作者或其他开发者作用非常大,因为当程序越来越长之后,无论是其他人或者作者自己要直接看懂都会很困难。适当的注释可以帮助别人和自己更好地维护程序。大家一定要学会并坚持写好注释的习惯。
Scratch里可以在每个指令上面点击鼠标右键,然后选择“添加注释”来给指令加上注释。

二次函数
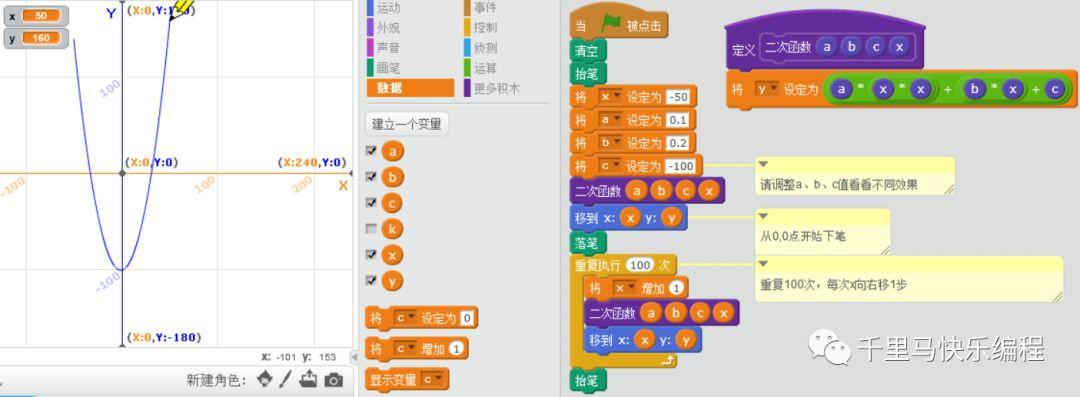
二次函数公式如下:
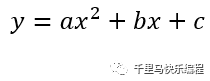
在Scratch里画出来的效果是一条抛物线(或反过来的抛物线),就像你把物品抛向空中再落下来的效果。
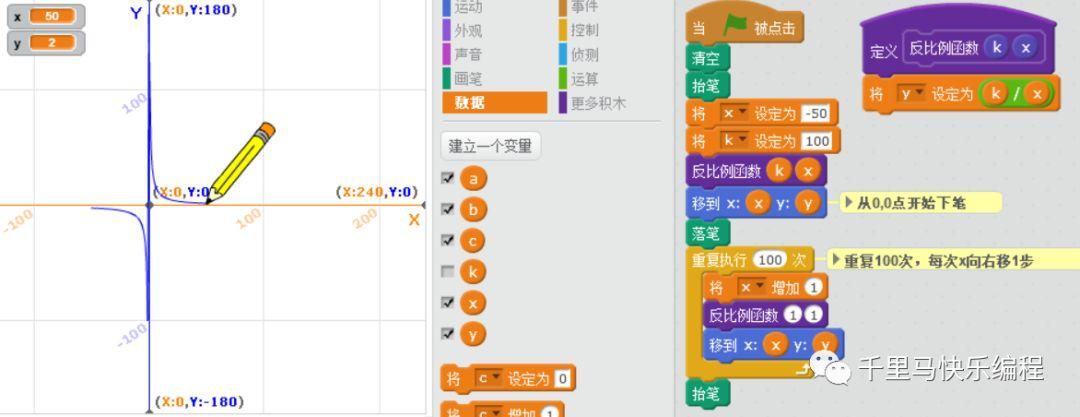
反比例函数
y = k/x
画出来是一条双曲线:
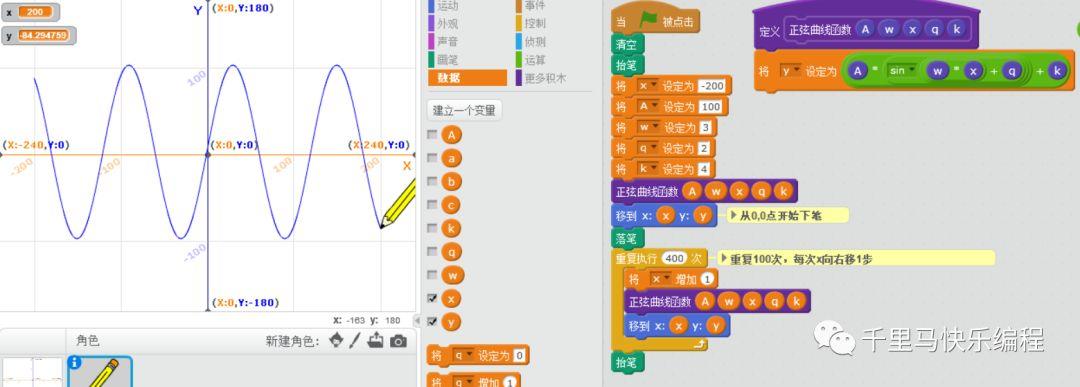
正弦曲线
接下来我们开始画一些和三角函数相关的曲线。Scratch里可以有三角函数方法,可以直接使用。
正弦曲线函数可表示为y=Asin(wx+q)+k。能想到现实中的正弦曲线吗?(心电图、电流图等)
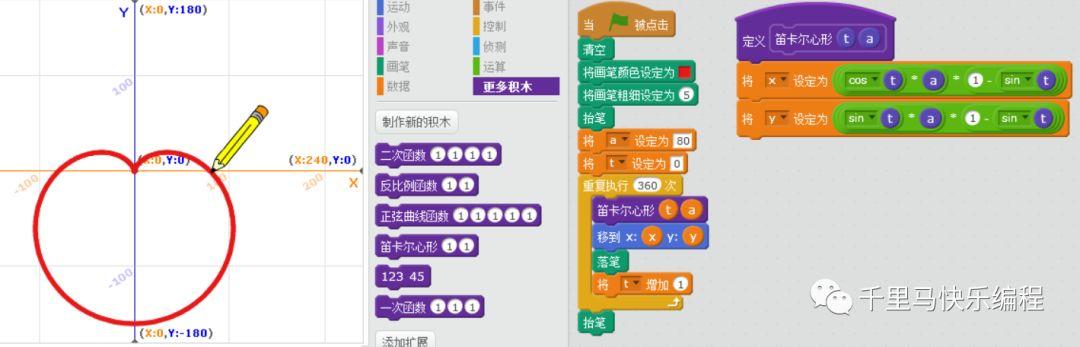
笛卡尔心形
笛卡尔心形的极坐标公式非常简洁:r=a(1-sinθ)
转换成直角坐标后,变成下面的函数:
x = cost * a (1 – sint)
y = sint * a (1 – sint)
其中a是控制心形大小的常量。t为角度参数,通过让其转一圈即从0-360度来完成画作。
以下就是完整程序和效果:
在历史上,笛卡尔和克里斯蒂娜的确有过交情。但笛卡尔是1649年10月4日应克里斯蒂娜邀请才来到瑞典,而当时克里斯蒂娜已成为了瑞典女王。本文开始的故事其实是后人为了纪念笛卡尔对于数学的杰出贡献而杜撰的。
后人对笛卡尔心形图函数也做过改进令其更加像爱心。比如下面这个桃心形函数:
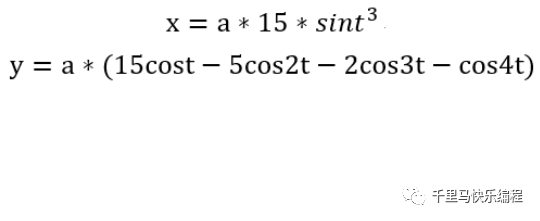

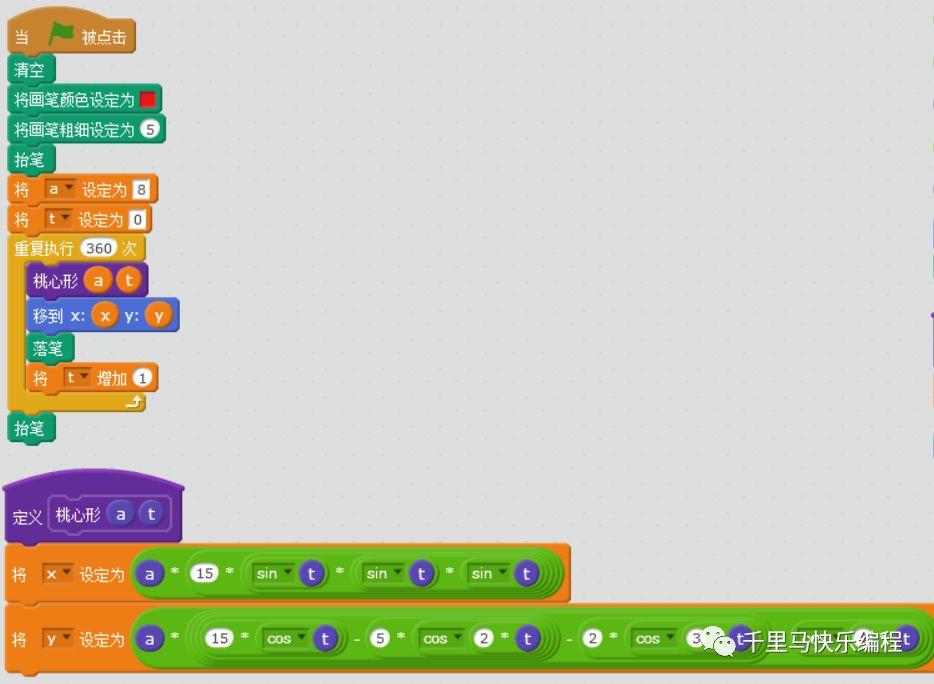
注意和笛卡尔心形一样,参数a控制心形大小,参数t是角度,必须要画完整一圈360度心形才完整哦。
蝴蝶曲线
最后给大家一个蝴蝶曲线函数:
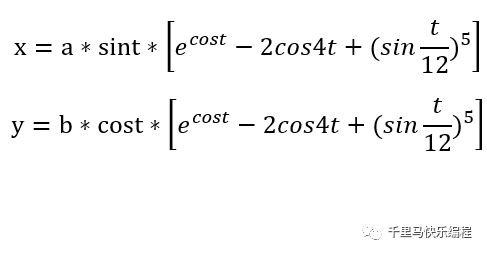

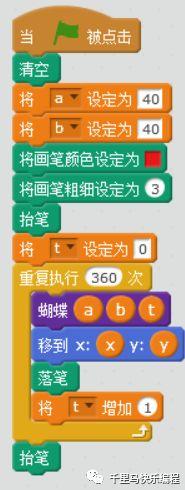
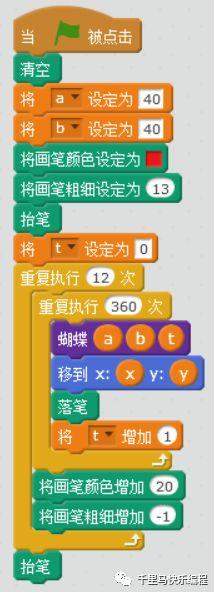
上面是画一个周期(360度)的蝴蝶曲线。大家也可以尝试多画几个周期,每个周期改变一下画笔颜色和大小,画出色彩斑斓的不同蝴蝶吧:


大家既要学会数学的函数,也要学好编程的函数哦。祝大家劳动节快乐!

