友情提示：680元/半年，儿童学编程，就上码丁实验室。
上一期提到了麦克劳林级数，其实它是泰勒级数的特殊形式。今天来谈谈泰勒级数的一个应用：精确的计算圆周率Pi。
数学公式：
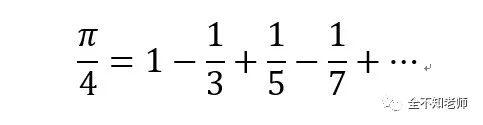
假设我们希望计算结果精确到小数点后第7位。考察1/(2n-1)的值，
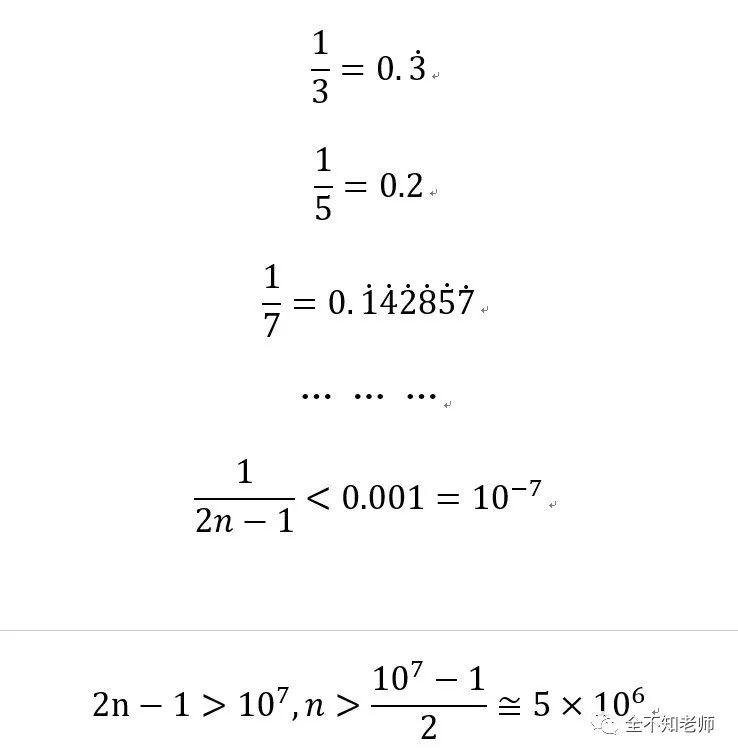
也就是说，n最少要取到5百万以上，才可以不考虑后面的项数产生的影响。
程序实现：
下面我们用程序来实现一下。这里选用Scratch，只给出了计算部分。
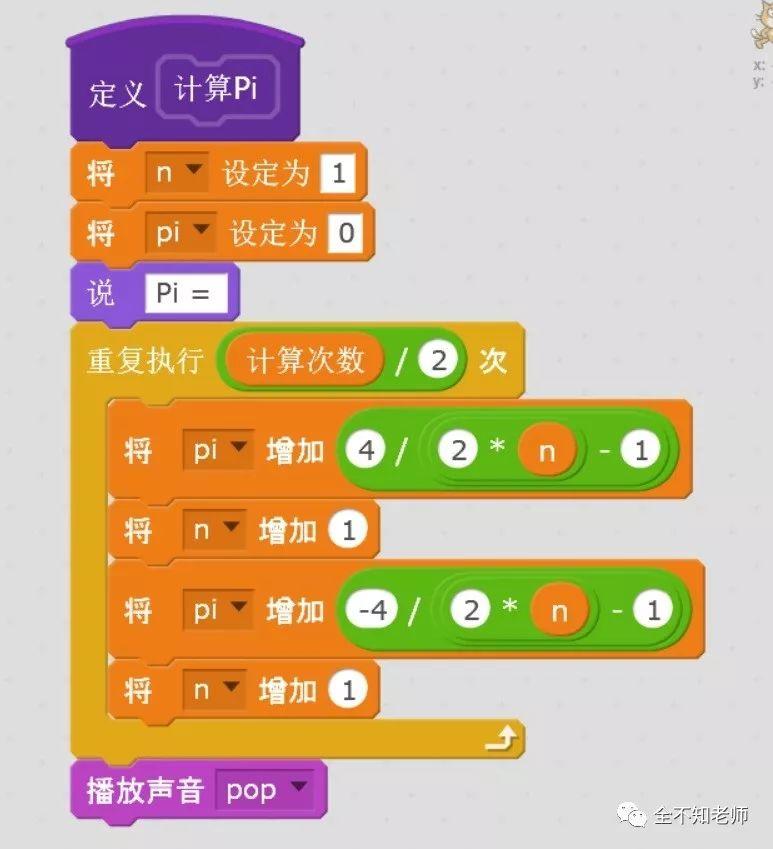
其中，变量n对应自然数，变量Pi对应计算的圆周率。根据精度要求的不同，给出不同的计算次数。
由于求和是交错的方式，即一加一减，程序实现时，分别进行了+4/(2n-1)和-4/(2n+1)的累加。
乘以4，是因为给出的公式是求π/4。
根据计算次数的不同，可以得到不同精度的π值：
1千次：3.140593
1万次：3.141493
十万次：3.141583
一百万次：3.141592
如下是计算视频：
为了能更好的动态展示累加过程，特意将显示部分放入循环体内。这样每次循环都会显示计算结果，具体视频如下：
可以看出，采用泰勒级数计算圆周率，收敛的速度很慢。
后记：由于计算精度有限，舍弃后面的项数，产生的误差称为截断误差。由于计算机字长有限，不能精确的表示数，产生的误差称为舍入误差。采用计算机程序来进行数值计算时，这是必须考虑的问题。在给出的示例中，由于Scratch只显示小数点后6位，所以50万次以上的计算结果都相同。想要得到圆周率后面更多的位数，需要采取其他特殊手段。
始发于微信公众号：
全不知老师