友情提示：380元/半年，儿童学编程，就上码丁实验室。
算24点是个经典的小游戏：从一副扑克牌中任意抽取4张牌，只利用加减乘除算出24，其中J、Q和K都算作10点。
为了简单起见，我们只考虑数字1-9，不考虑10和J、Q、K。
在这些有些组合中，有的无解，例如1、1、1、1。有的有很多解，例如8、5、4、7，有66组解。有的必须带括号，例如1、4、7、9，解法为：(9-1)*(7-4)。
这个题目一般作为小学1-2年级的奥数题目，用来加强学生对加减法和乘除法的掌握。
例如，最常考虑的解法，是四个数字求和。其次，是凑出24的两个因子，例如3和8，4和6，或者2和12，然后相乘。
然而这却是一道地地道道的编程题目，其中涉及若干编程技巧。
技巧一：枚举法。
加、减、乘、除作为四则运算，在编程的表达式分类中属于一大类别：二目运算符。即必须有两个数(或值)参与运算。
因此，四个数之间，需要放置三个运算符。由于每个位置可以放置四种运算符中的一种，因此有4×4×4=64种情形。
对于编程而言，就是简单的三重循环。如下图所示：
其中op_i、op_j和op_k分别代表外、中、内三重循环的循环变量。op是运算符(operator)的字头缩写。
技巧二：括号的考虑
我们知道四则运算是有优先级的，没有括号时，要先乘除后加减。如何处理括号，是算24程序的一大难点。
考虑到它们都是二目运算符，所以这里采用强制括号的方法来处理。所谓强制括号，就是不管其他运算符如何，将当前运算符两边加上括号。
例如，考虑8、5、4、7求24。计算8和5时，在中间分别填上+、-、*和/号后，将计算结果保留，然后参与后续的运算。相当于在算式两边加上了括号。
例如，第一个位置和第二个位置的完整程序如下：
其中n_r1、n_r2、n_r3存放每个二目运算符的中间结果。例如第一个数字和第二个数字的运算结果为n_r1，然后n_r1与第三个数字运算，结果为n_r2。
另外，关于“运算符的转换”，这里涉及Scratch的一个特殊之处。
Scratch是无法传递参数的，也没有返回值。因此采用全局变量的方式编制了一个公共子程序。让op_a存放第一个数字，op_b存放第二个数字，op_op里存放具体的运算符，将运算结果存放在op_c里。
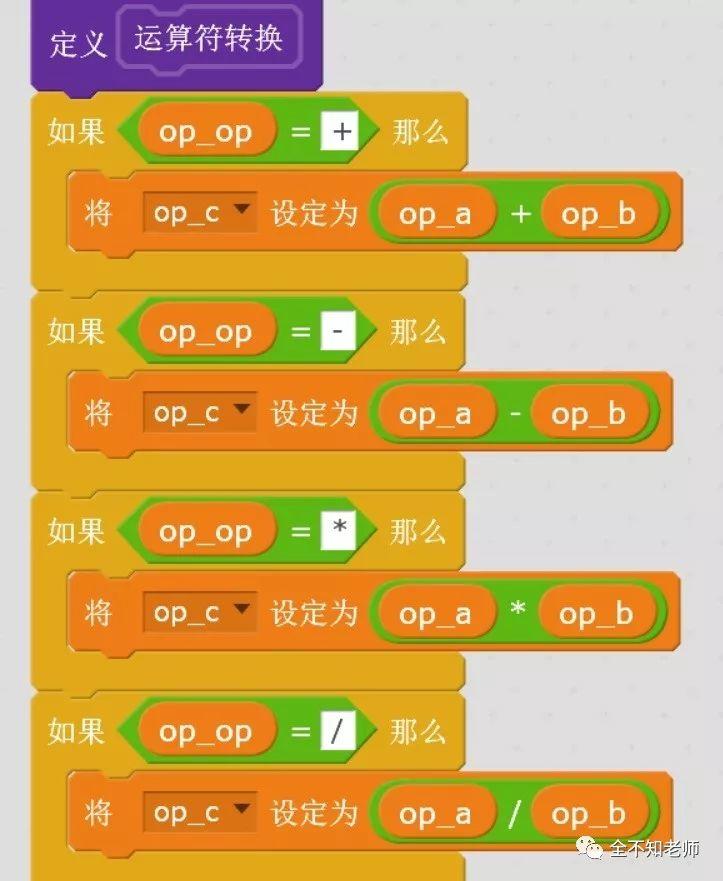
这种处理方式，同时解决了加、减、乘、除四个运算符的转换问题。因为Scratch不支持数据的类型转换，通过生成一个表达式来求值是行不通。
括号的处理，除了前述的((数字1〇数字2)〇数字3)〇数字4的形式以外，其中〇表示四则运算算子，还有(数字1〇数字2)〇(数字3〇数字4)的形式。例如(9-1)*(7-4)。
因此在括号处理上，要考虑双左括号和一左一右两个括号，这两种情形。其他情形通过对四个数字的完全排列都可以转化为这两种情形。
技巧三：四个数字的全排列。
由于没有限定数字的顺序，必须对给定的四个数字做全排列，针对每个排列，利用前述的算符枚举，才能求出所有的解。
全排列问题是一个更为经典的编程题目，据说很多IT公司面试时会考查。
全排列问题，有递归法和非递归法两类算法。由于Scratch不支持参数传递，无法采用递归法。
因为递归法的基本思想是：先把一个四个数的全排列问题，转化为每个数开头，然后后面3个数的全排列问题。这样依次类推。
非递归算法就相当啰嗦，计划单开一个专题讨论。
其实对于算24的问题规模，4个数字有4！=24种排列。直接给出这24个排列，然后一一调用“算符枚举”，也不失为一个简单可行的办法。
程序运行实例：如图所示：
给定8、7、6、9，算24。
有2组解。
分别是：(8*6)/(9-7)和(6*8)/(9-7)。
更多计算实例参见视频。
后记：算24问题，算符有64种可能，数字有24种可能，括号有2种填法，因此该问题总共有：64×24×2=3072种可能。
如果不限定只采用加减乘除四种运算符，该问题其实有个万能解：
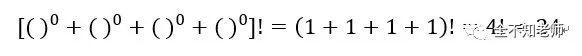
因为任何数的零次方为1，四个1的和为4，而4的阶乘为24。
始发于微信公众号：
全不知老师