友情提示：680元/半年，儿童学编程，就上码丁实验室。
π是一个重要的常数，表示圆的周长与直径之比，π对于计算圆的周长和面积等有重要的作用。古代人从很早就开始意识到π的意义。但是由于古代时的计算手段和计算方法比较落后，所以π的计算在当时是比较困难的。现在随着计算机的发展，计算能力有了极大的提高，计算出准确的π已经是很容易的事情了。
今天我们就来研究一下，在Scratch中如何使用割圆法得到PI。让我们与历史上的科学家一起，重温一下求π之路。
我们先看一下割圆法的算法。
在一个圆内做内切的正N边形，随N的增大，多边形的形状会逐渐接近于圆，多边形的边长也就逐渐趋近于圆的周长。求出多边形的周长和面积，就近似得到了圆的周长和面积，能够计算出π。
首先，我们用下面的程序演示一下割圆法的原理。
建立两个全局变量N和r。在舞台中初始化及用上下键调节N的大小。
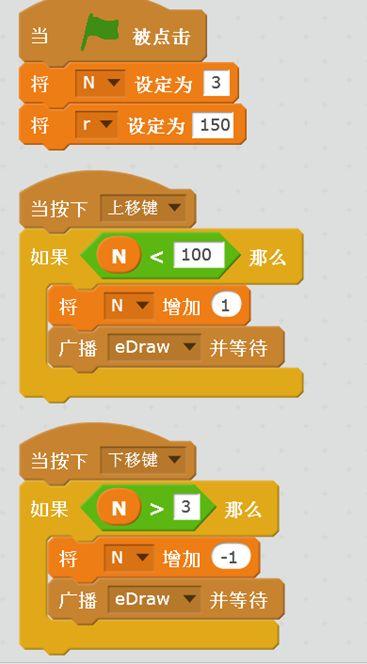
在角色中响应消息绘图。要绘制N边形，则每一边对应的角度为360/N度。所以每次将角度a增加360/N就可以得到多边形的各个顶点对应的角度，顶点的坐标可以通过x=r*cos(a)与y=r*sin(a)计算。将各个顶点连接起来就绘制出了多边形。程序如下：
下面动画演示了从N=3到N=40时的正多边形（绘圆的程序略去）。
可以看到，当N增大时多边形与圆形逐渐接近。可以想象，如果N增加到无穷大，多边形就会与圆重合。
下面，我们再利用这个方法计算π。
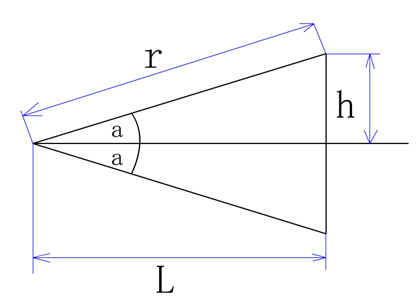
根据这种思想，我们可以计算一下，不同N时，得到的边长是多少，以及计算出的π值是多少。
我们用下面的程序来计算不同N时的π值。
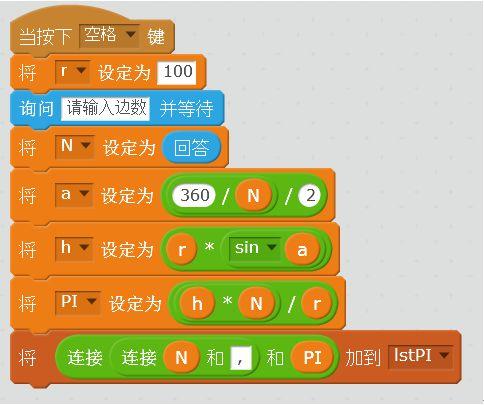
经过改变N进行计算，得到了下面的结果。下面是从N=3开始，每次乘以2得到边数计算的π值。
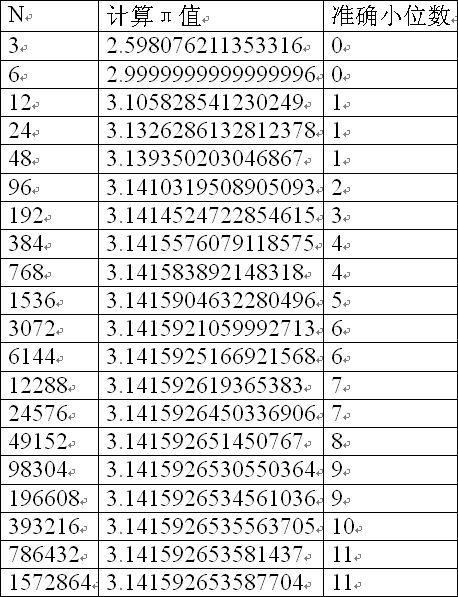
可以看到我们计算出的π值已经十分准确了。
总结
1 使用割圆法计算了π，由于现在的计算机所拥有的计算能力，能够比较快地得到准确的结果。
2 这种朴素方法的思路中包含了无限及求极限的思想。一方面通过不断增加N可以越来越接近圆形。另一方面，在精度不高的情况下，我们往往可以使用多边形来代替圆。实际上很多时候在Scratch中绘制圆形都是用的这种方法。
3 这个算法只是求π多种方法中的一种，以后有机会，我们还会介绍其它求π的算法。
1 公元263年，中国数学家刘徽用“割圆术”计算圆周率，他先从圆内接正六边形，逐次分割一直算到圆内接正192边形得到了π=3.14的圆周率近似值，3.14这个数值还是偏小。于是继续割圆到1536边形，求出3072边形的面积，得到令自己满意的圆周率3.1416。
2 公元480年左右，南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果，给出不足近似值3.1415926和过剩近似值3.1415927，还得到两个近似分数值，密率355/113和约率22/7。
3 德国数学家鲁道夫·范·科伊伦（Ludolph van Ceulen）于1596年将π值算到20位小数值，后投入毕生精力，于1610年算到小数后35位数，该数值被用他的名字称为鲁道夫数。（在现在的计算机上，计算出这样精度的结果可能只需要几秒钟的时间）。
4 π的前100位为3.1415926535 8979323846 26433832795028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679