Scratch教程：经典欧几里德算法的Scratch实现

欧几里德算法是一个经典的数学算法。这个算法在很多计算机算法教材中被作为第一个算法而进行讲解。同时这个算法也是教育部新编的教学大纲，《普通高中信息技术课程标准（2017版）》中的要求内容。

 

首先我们来了解一下欧几里德及他的算法。

欧几里得

欧几里得（公元前330年—公元前275年），古希腊数学家。他活跃于托勒密一世（公元前364年－公元前283年）时期的亚历山大里亚，被称为“几何之父”，他最著名的著作《几何原本》是欧洲数学的基础，提出五大公设，欧几里得几何，被广泛的认为是历史上最成功的教科书。欧几里得也写了一些关于透视、圆锥曲线、球面几何学及数论的作品。

欧几里德算法又称辗转相除法，是指用于计算两个正整数a，b的最大公约数。是由欧几里德在其著作《The Elements》中最早描述了这种算法,所以被命名为欧几里德算法。

算法的计算公式是gcd(a,b) = gcd(b,a mod b)。即在输入a和b后，程序计算a除以b的余数，如果余数为0，则b就是最大公约数。如果r不为0，则把b赋给a,把r赋给b，反复进行计算，直到得到结果为止。

 

 

作为一个数学的算法应该具有如下的特征：

 

 

1有穷性（Finiteness）

算法的有穷性是指算法必须能在执行有限个步骤之后终止；

 

2确切性(Definiteness)

算法的每一步骤必须有确切的定义；

 

3输入项 (Input)

一个算法有0个或多个输入，以刻画运算对象的初始情况，所谓0个输入是指算法本身定出了初始条件；

 

4输出项 (Output)

一个算法有一个或多个输出，以反映对输入数据加工后的结果。没有输出的算法是毫无意义的；

 

5可行性(Effectiveness)

算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步，即每个计算步都可以在有限时间内完成（也称之为有效性）。

 

可以看到，欧几里德算法是符合上述算法要求的。它有两个输入变量及一个输出变量，每一步骤都是确切的，也是可行及有穷的。

 

下面，我们研究一下，如何在Scratch中实现这个经典的算法呢？

首先我们使用框图描述这个算法，这也是使用计算机实现算法的常用方法。根据算法的描述，我们可以绘出两个稍有不同的框图。

框图1是计算余数，之后判断余数，如果余数为0，则从中间退出循环。

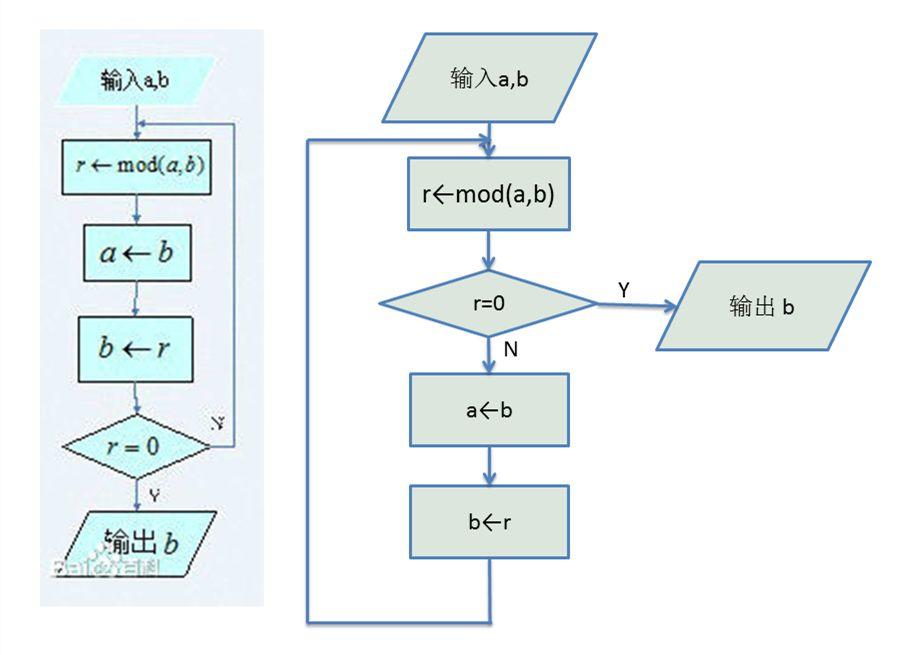
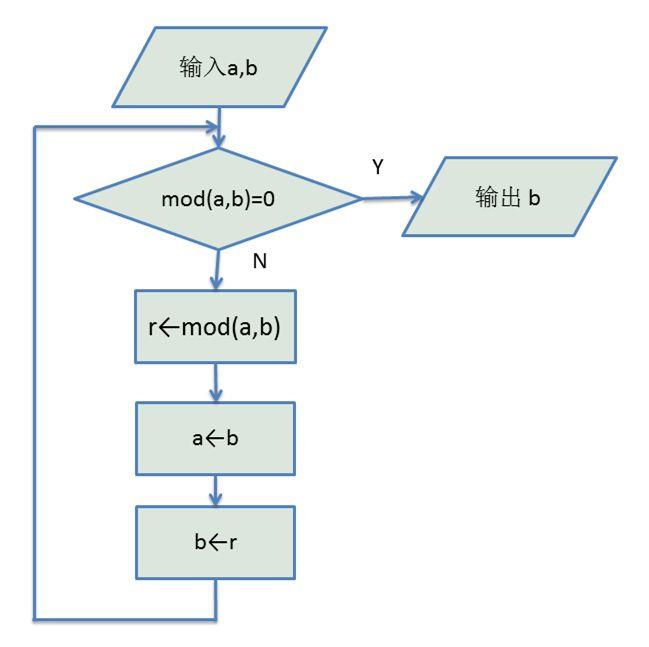框图2 是在循环的入口进行条件检查，之后再进行计算。

这两个流程图实现的功能是一样的。但在实现的复杂程度和效率上是有差别的。

 

下面我们在Scratch中分别实现这两个流程。

首先，我们定义几个变量 a,b,和r。开始时输入a,b。之后使用一个自定义积木完成算法。

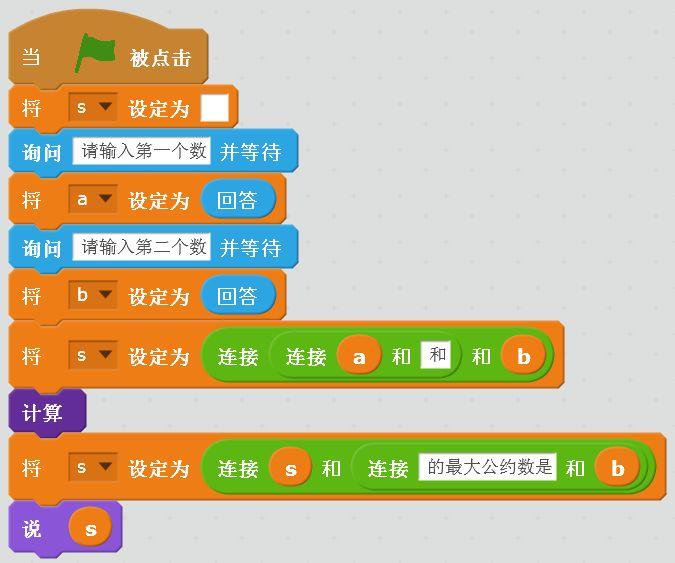
对应于框图1，可以使用如下的程序完成

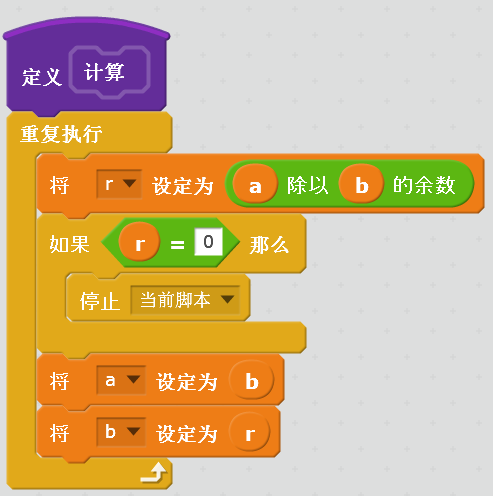
需要注意：这里利用了在循环中间根据条件退出循环，在Scratch中就是停止当前脚本（也就是当前自定义积木）。如果不使用自定义积木，在主程序中也可以实现，但方法比较复杂一些，大家可以自己考虑试做下。

对应于框图2，可以使用如下的方式实现。

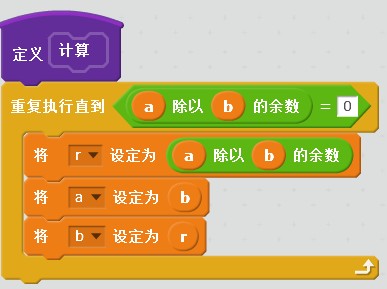
注意在这种实现方法中，使用的循环语句与第一种方式不同，可以比较容易地嵌入主程序中。但也应该注意：

与第一种方法相比，第二种方法在每次循环时，计算了两次余数。增大了计算量。可能你会说“这个对运行没有什么影响啊？”。但对于大量的计算而言，需要尽可能地提高算法的效率，减少计算量。这是作为一个程序设计者必须要进行考虑的。当然，也可以处理成只计算一次余数，大家同样可以试做一下。

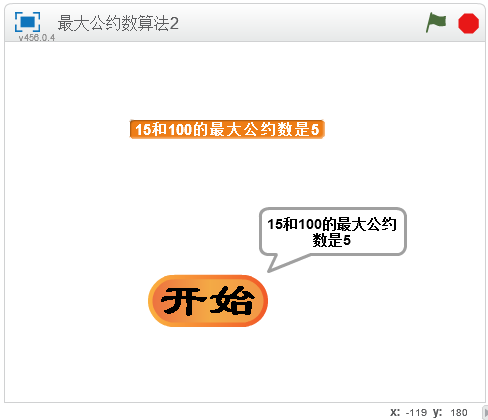
运行输入两个数值后，就可以计算出两个数的最大公约数。

 

 

总结

 

1

 

  在用计算机实现数学算法时，必须保证算法满足几个特征，否则可能无法编程完成。

2

同样的算法，可能使用不同的流程及方法来实现。

3

“信息技术课程标准”中提到了“体验算法效率的差别”及“会计算算法的时空复杂度“。在我们算法的实现中，就比较了两个不同方式的程序复杂度和运行时间。