Python：海龟绘图（四）

上节课的作业是：从绘制正八边形改为绘制正二十边形，能否只修改一个参数，就达到同时修改“循环次数”和“旋转角度”的目的呢？

 

给出的提示是：定义一个与“循环次数”和“旋转角度”都有关的变量。这个变量应该是什么呢？

 

首先考虑“循环次数”，这个由什么决定？我们的做法一直是“绘制多少边形，就循环多少次”。所以，“循环次数”是由多边形的边数直接决定的。

 

那么“旋转角度”是否也与多边形的边数有关呢？经过分析前面四边形、五边形、八边形的程序，我们发现，随着边数的增多，旋转角度一直在减小。事实上，我们每次修改的旋转角度，正是由公式“360➗N”计算出来的，而这个“N”，不正是多边形的边数吗！

 

所以，这个与“循环次数”和“旋转角度”都有关的变量就是“边数”。搞明白这个，程序修改起来就很简单了，分为四步（比“把大象放冰箱里的步骤”多一步）：

 

（1）定义变量“sides”表示“边数”,并赋初始值“8”；

（2）将“range(8)”中的“8”，替换为变量“sides”；

（3）将“t.right(angle)”中的“angle”，替换为“360/sides”；

  (4)  由于变量“angle”已完成了其历史使命，可以功成身退了，故可将“angle = 45”那行直接删去，或是在该行的行首加上一个“#”，将这一行改为“注释”（万一以后还用得着呢）。

 

修改后的程序如下：

 

有了这个全新版框架，画个正二十边形试试！只需把“8”改为“20”，走起！……等会儿，怎么会这样？

好像是小海龟这一圈“兜得有点儿大”，怎么办呢？

我们来分析一下：和绘制正八边形的程序相比，我们只是将边数从“8”改为了“20”，每边的边长没有变，仍然是“50”，那这一圈的总长度（专业术语叫“周长”）就从“50*8”变为了“50*20”，自然就“大”了，大得出了窗口边界，大得都只剩下一半了！然而边数肯定是不能减的，要不怎么叫“二十边形”呢！看来只能从“边长”入手了。

现在我们希望“随着边数的增大，边长越来越小”，即希望“边长与边数成反比”。由于有公式“边长*边数=周长”，故控制住了“周长”，也就控制住了“边长”。根据之前的经验，周长设定为“500”较为合适，故边长应为“500/边数”。

由此，我们修改程序如下：

现在我们回过头将最新版程序与最初的正方形程序对比一下：

 

不难看出，最初的程序有点“大白话”的感觉，就是想做什么直接罗列上去，比较“简单粗暴”。而现在的程序，已经由丑小鸭变成了白天鹅，想绘制多少边形只需要修改“边数”，而把“旋转角”、“边长”什么的统统交给程序“自己”去计算，通用性已大为提高，甚至具有了某种程度的“美感”。

 

这个程序代码的转变过程，同时也是从“人类思维”到“计算机思维”的转变过程，其中体现的就是“程序设计思想”。学会写这几句代码其实并不难，大可以“照猫画虎”甚至“死记硬背”。所以，学会写代码不是我们课程的终极目标。

 

真正困难的，是学会“程序设计思想”，也就是遇到一个问题，怎么用计算机的思维去思考、去解决，而不是用人类的思维方式。这绝非一朝一夕之功，但也并非难以企及。代码写多了，想多了，悟多了，自然就慢慢的形成了。这才是我们的公众号努力的方向，虽然限于水平可能不一定能达到，但我们会一直奔着这个目标努力下去！

 

至此，“正多边形”已经被我们彻底“玩明白了”，下面我们要换个玩法，尝试一些新的“变化”。变什么呢？我们先来变“边长”。

 

在正多边形中，无论边长是咱们指定的还是程序计算的，每边的长度都是相等的，是所谓“正”。如果每边的长度都不相等会怎么样，比如每条边的长度都比前一条边长一点？

 

让我们试一下。增加一个变量“length”，代表“边长”。将初始边长设为“2”，每条边比前一条边增加2步，也就是“每次移动length步，然后再给length加2”，先循环个10次试试，修改代码如下：

 

得到的效果如下图。注意一下代码中红框标出的部分，您可能觉得这行代码肯定是写错了，这个等式在数学中根本不成立啊！一个变量怎么可能等于这个变量再加上2呢？等式两边同时减去这个变量，岂不是得到“0 = 2”？显然不成立啊！

 

我要说，您分析的很对，如果把“=”当作“等号”，那么这个算式的确是错的。但在程序设计中，“=”绝大部分时候应理解为“赋值”操作，即把“=”右边的数值赋给“=”左边的变量。这样的话，红框里的语句应理解为“先用原来的length和2相加，把相加的结果赋给新的length”，这时新的length就比原来的length大了2，也就是自身的值增加了2。

 

这个语句更专业的写法是“length += 2”，其作用与“length = length + 2”完全相等。

 

 

看出规律了吗？将循环次数增加到100再试试！

 

 

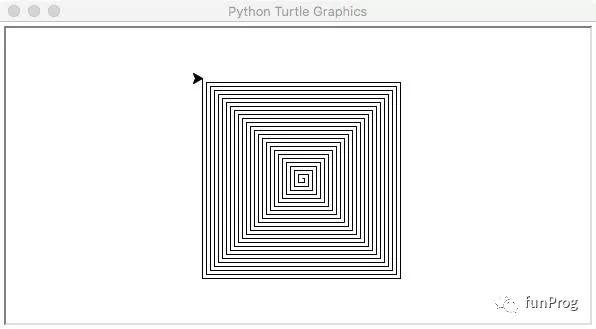
哇！都有点立体感了有木有！

项目小结：

在今天的项目中，我们：

1. 继续巩固了“变量”和“循环”的使用方法，用1个变量来控制正多边形绘制程序中所有的变化，使得程序的通用性大大提高；

2. 继正多边形后，探索了“渐变边长”图形的绘制方法，为海龟绘图的舞台增添了新鲜元素；

3. 通过将最新版程序与最初的正方形程序进行对比，初步探讨了“人类思维”与“计算机思维”的不同，以及学习“程序设计思想”的重要性；

 4.    学习了使变量自身的值增加的语句写法，更深入的理解“=”的意义

课后思考：

 

今天探索了“渐变边长”的图形绘制，程序中还有另一个重要变量——角度，如果在角度上“做点手脚”，又会产生什么神奇的效果呢？发挥您的想象力，尽情的探索吧！