友情提示：视频教程观看时请手动设置清晰度。
今天是系列一，用Scratch验证尼科梅彻斯定理。
任何一个整数的立方都可以写成一连串相邻奇数之和(因为如果不是一串相邻的奇数，这个奇数组合可能会有多个)，这就是著名的尼科梅彻斯定理。
假设这个整数用n表示，那么这一连串的奇数为从 n*n-n+1，到 n*n+n-1之间的奇数。
例如： 如果整数n=3，那么3的立方为 3*3*3=27
而 n*n-n+1=7，n*n+n-1=11，从7到11之间的奇数之和为 7 + 9 + 11 = 27 ，从而验证了尼科梅彻斯定理成立！
下面我们看看Scratch编程如何实现来验证这个定理吧。。
首先程序会询问验证的自然数，然后会把上面提及的这个自然数相关的奇数放到奇数列表中，最后如果这个自然数的立方等于奇数列表的各个项目之和，那么通过构造的字符串，宣告验证的数字符合尼科梅彻斯定理。
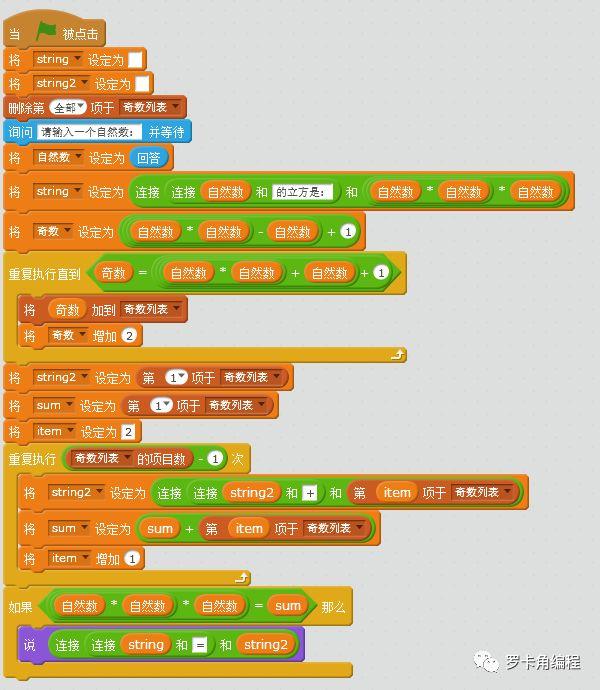
我们用自然数6来验证一下：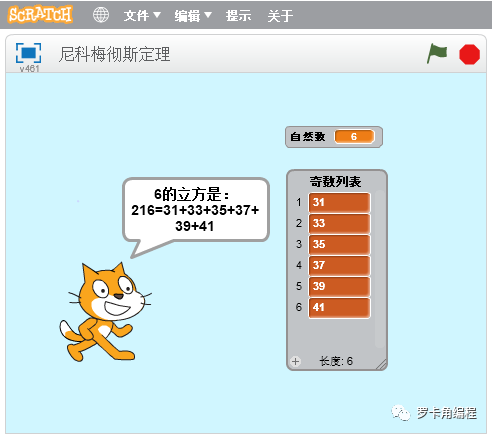
ok，验证成功了！
怎么样，你也来跟着试一试吧？