友情提示：视频教程观看时请手动设置清晰度。
阅读此文，您需要在之前熟悉以下内容：
函数（即自定义积木）
下面来看大家都熟悉的一一个民间故事:
从前有座山，山上有座庙，庙里有一个老和尚在给小和尚讲故事:
从前有座山，山上有座庙，庙里有一个老和尚在给小和尚讲故事:
从前有座山，山上有座庙，庙里有一个老和尚在给小和尚讲故事:
从前有座山，山上有座庙，庙里有一个老和尚在给小和尚讲故事:
……
显然，故事里包含了它本身。
视觉上：
图片的内容包含了本身
以上两个例子就类似于递归。
递归是一个很神奇的东西，
递归的定义如下：
如果你还没有明白递归是什么意思，参见递归。
或许你有些明白了，递归就是“自己调用自己”，且满足某一个条件时，退出递归，也就是必须存在一个能让递归调用退出的简单出口(称为边界条件),即递归不能无休止的进行下去。（上面例子的边界条件就是“如果你明白了递归的意思,就退出”）
基本思想：把问题分解成规模更小，但和原问题有着相同步骤解法的问题，即子问题。
从技术角度说，递归就是函数自己调用自己的行为，简化流程如下。
数学函数可以用递归定义：
例如，阶乘（所有小于及等于该数的正整数的积，并且0的阶乘为1。自然数n的阶乘写作n!）
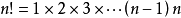
例如5的阶乘等于5×4×3×2×1=120
阶乘可以化成递归的形式
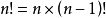
也就是n的阶乘等于n-1的阶乘再乘以n（好好理解）
当然，特别的，0的阶乘等于1，这也是我们递归的终止条件。
用scratch实现也很简单
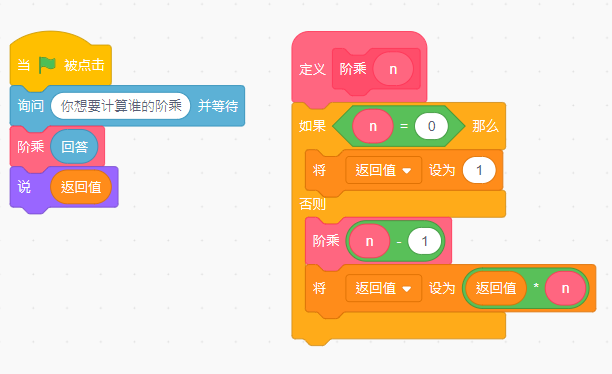
如果还不能理解上面的例子的实现，让我来打个比方：
皇帝：大臣，给我算一下3的阶乘
大臣：知府，给我算一下2的阶乘
知府：县令，给我算一下1的阶乘
县令：师爷，给我算一下0的阶乘
师爷：回老爷，0的阶乘等于1
县令（心算，1的阶乘等于0的阶乘1）：回知府大人，1的阶乘等于1
知府（心算，2的阶乘等于1的阶乘2）：回大人，2的阶乘等于2
大臣（心算，3的阶乘等于2的阶乘3）：回皇上，3的阶乘等于6
皇帝满意了
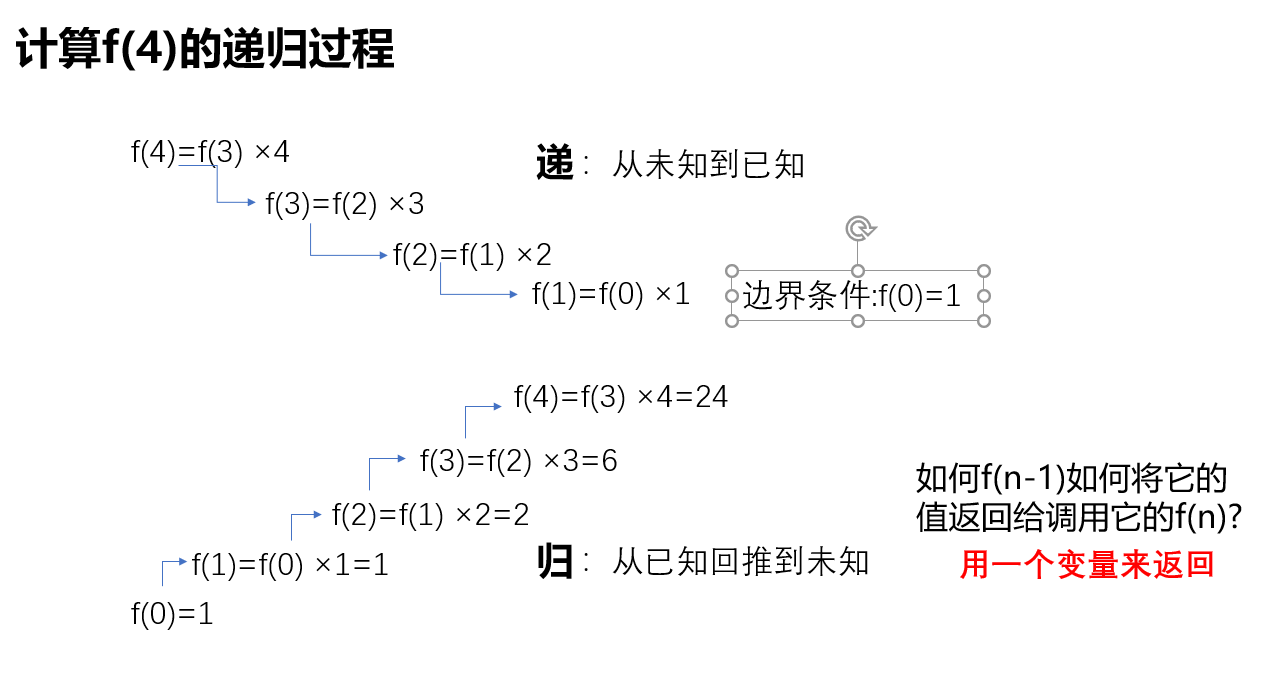
再用图片演示一下
如果用f(x)来表示递归求阶乘的函数
那么f(4)（4的阶乘）的求解过程用图像表示就是
理解上面递归例子之后，我们来看一个进阶例子：
汉诺塔相信大家都有所了解。
汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
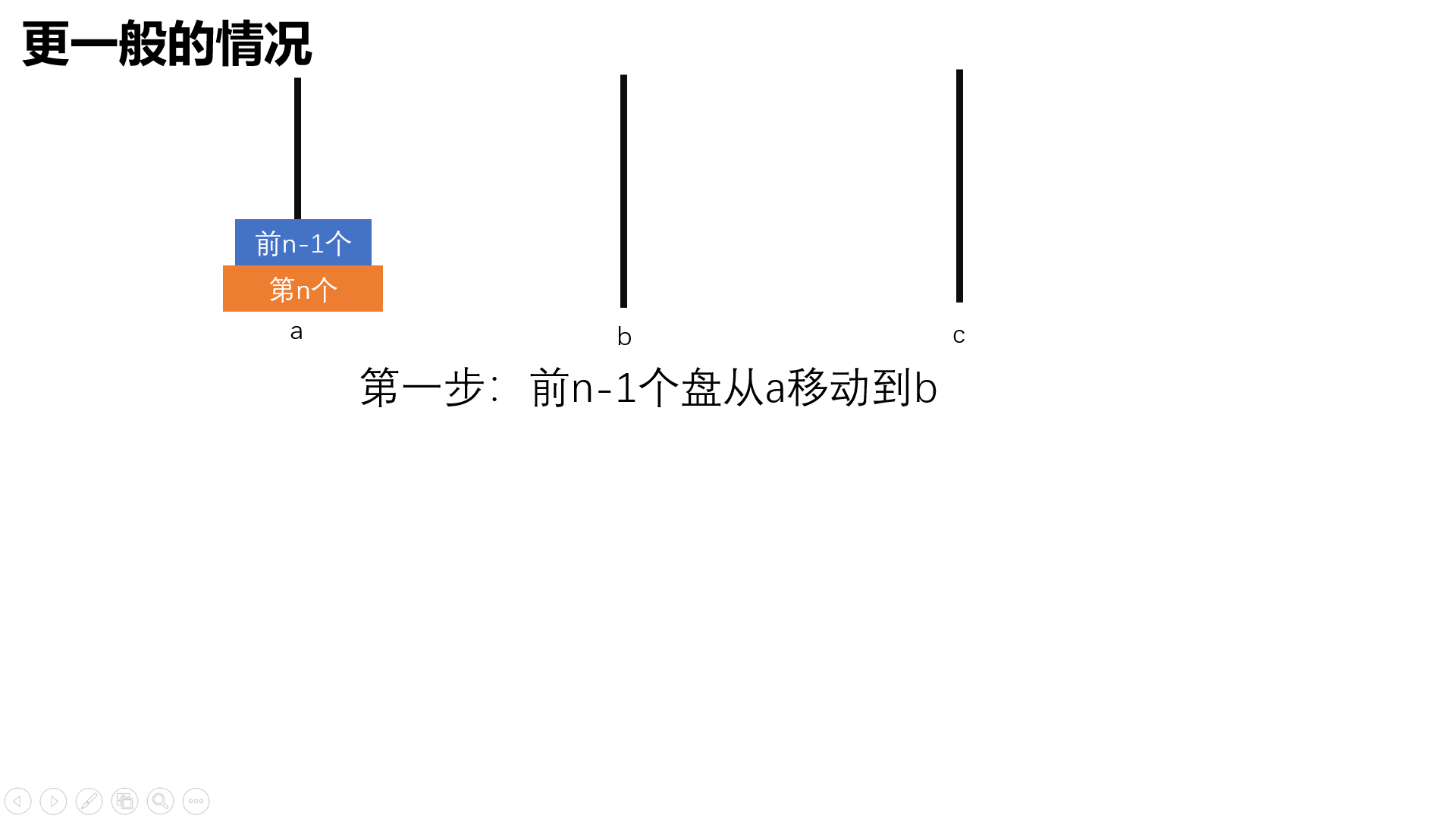
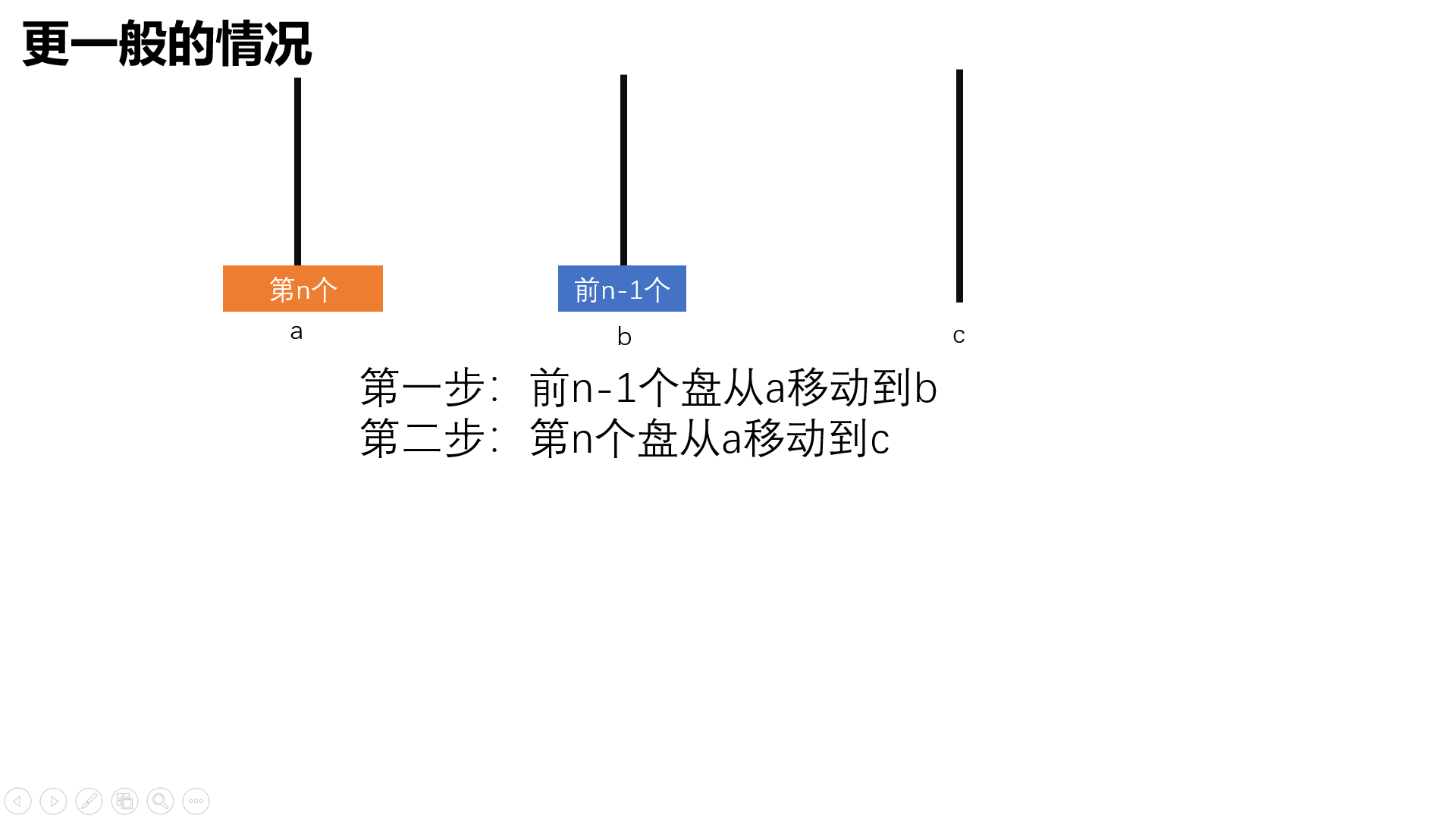
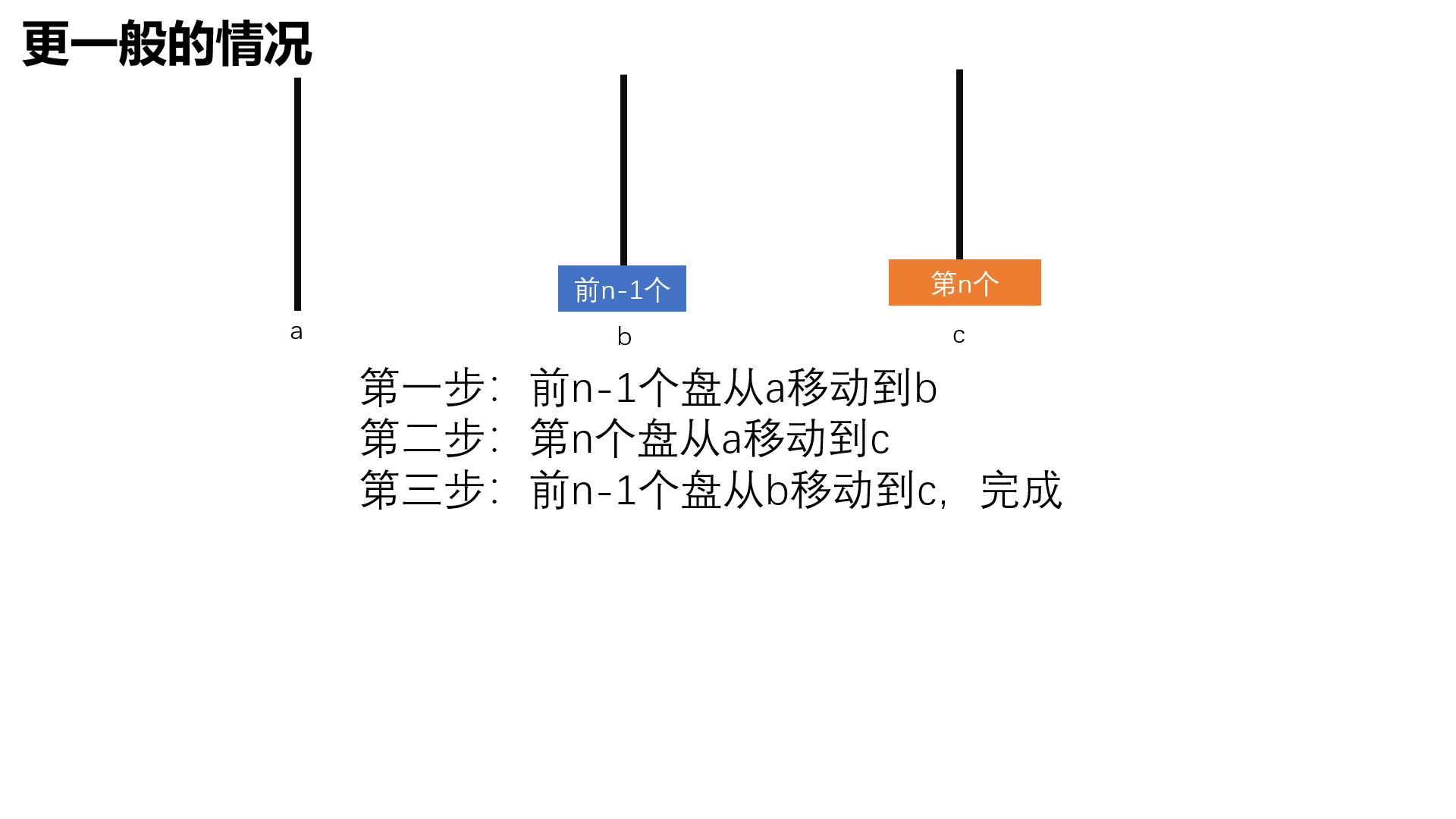
更规范详细地描述汉诺塔问题
设a，b，c是三个塔座，开始时，在塔座a上有一叠共n个圆盘，这些圆盘自下而上，由大到小地叠放在一起，各圆盘从小到大编号为1，2,3，…，n。现要求将塔座a上的一叠圆盘移到塔座c上，并仍按同样顺序叠置。在移动圆盘是应遵守以下移动规则：
（1）每次只能移动一个圆盘；
（2）任何时刻都不允许将较大的圆盘压在较小的圆盘之上；
（3）在满足移动规则（1）和（2）的前提下，可以将圆盘移至a，b，c中任一塔座上。
要求说出若干盘子的移动方法，如a->b表示将a塔座顶端地盘子移到c塔座
如果还不懂，可以看一下下面完整版汉诺塔作品（来自科技传播坊）
推荐输入3或4.观察运行情况，了解规则，先不用关心脚本如何实现。
有没有思路来解这道看似很有趣但很难的题，
这就要有情我们的伟大的递归出场了！
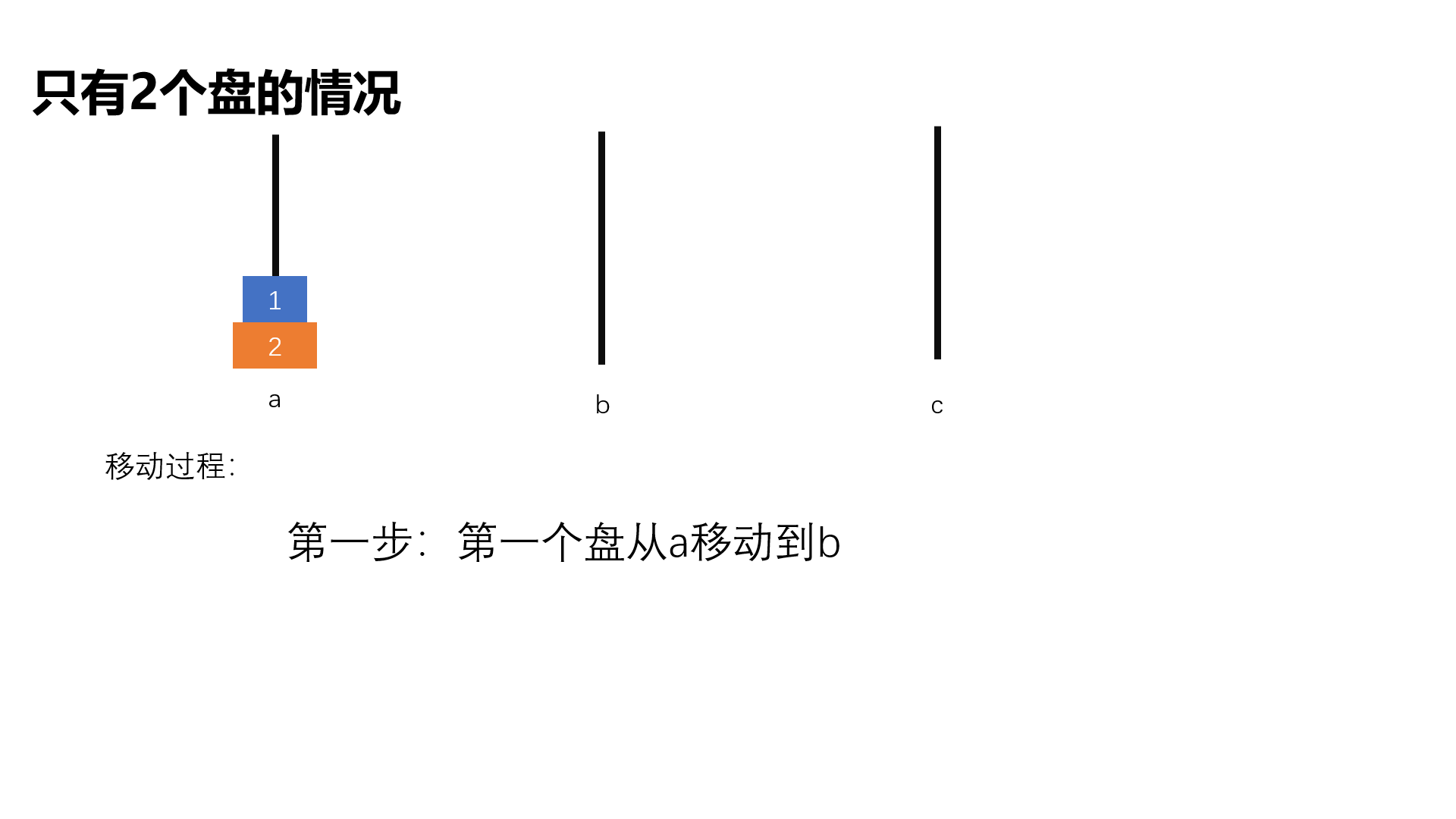
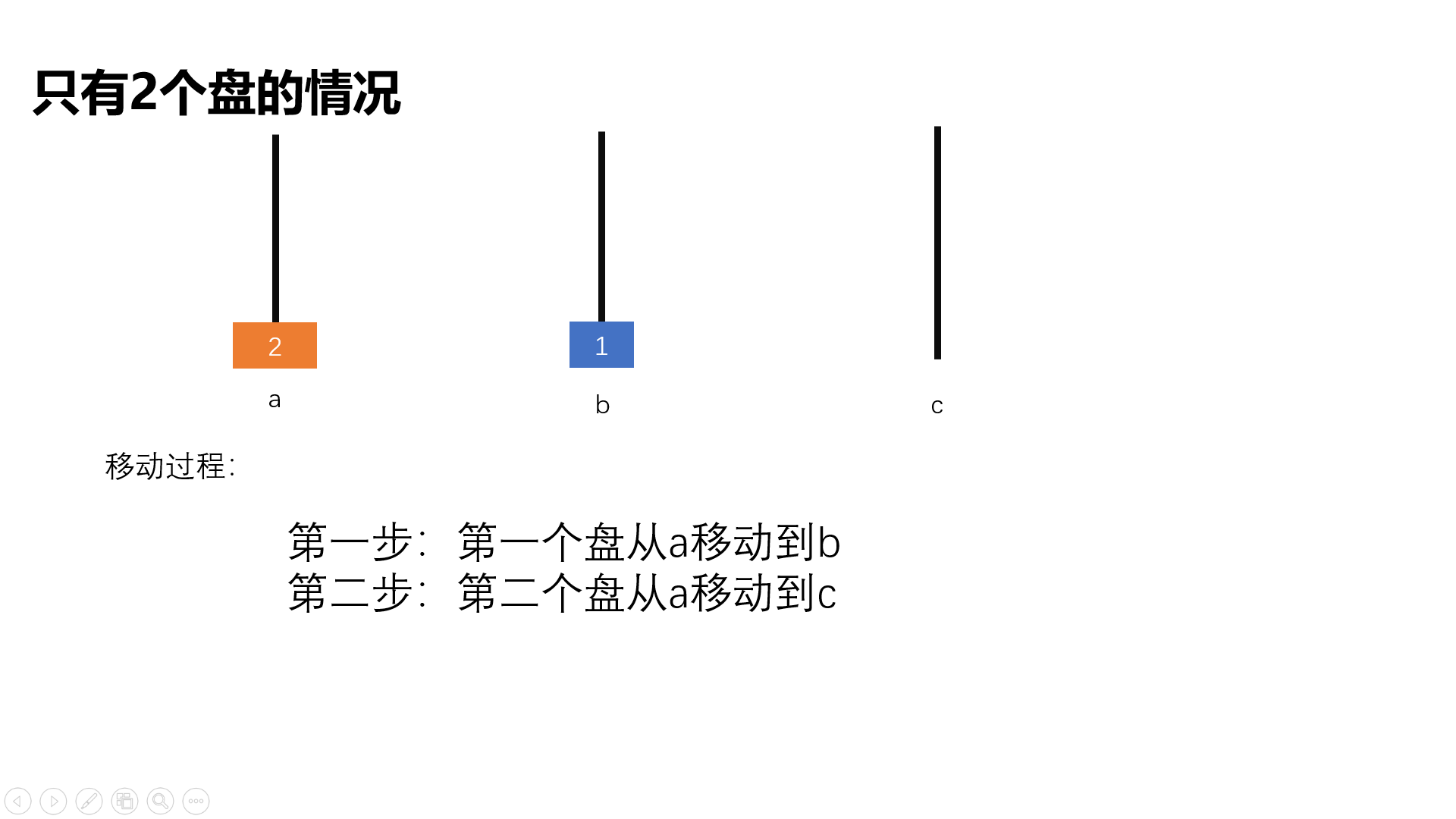
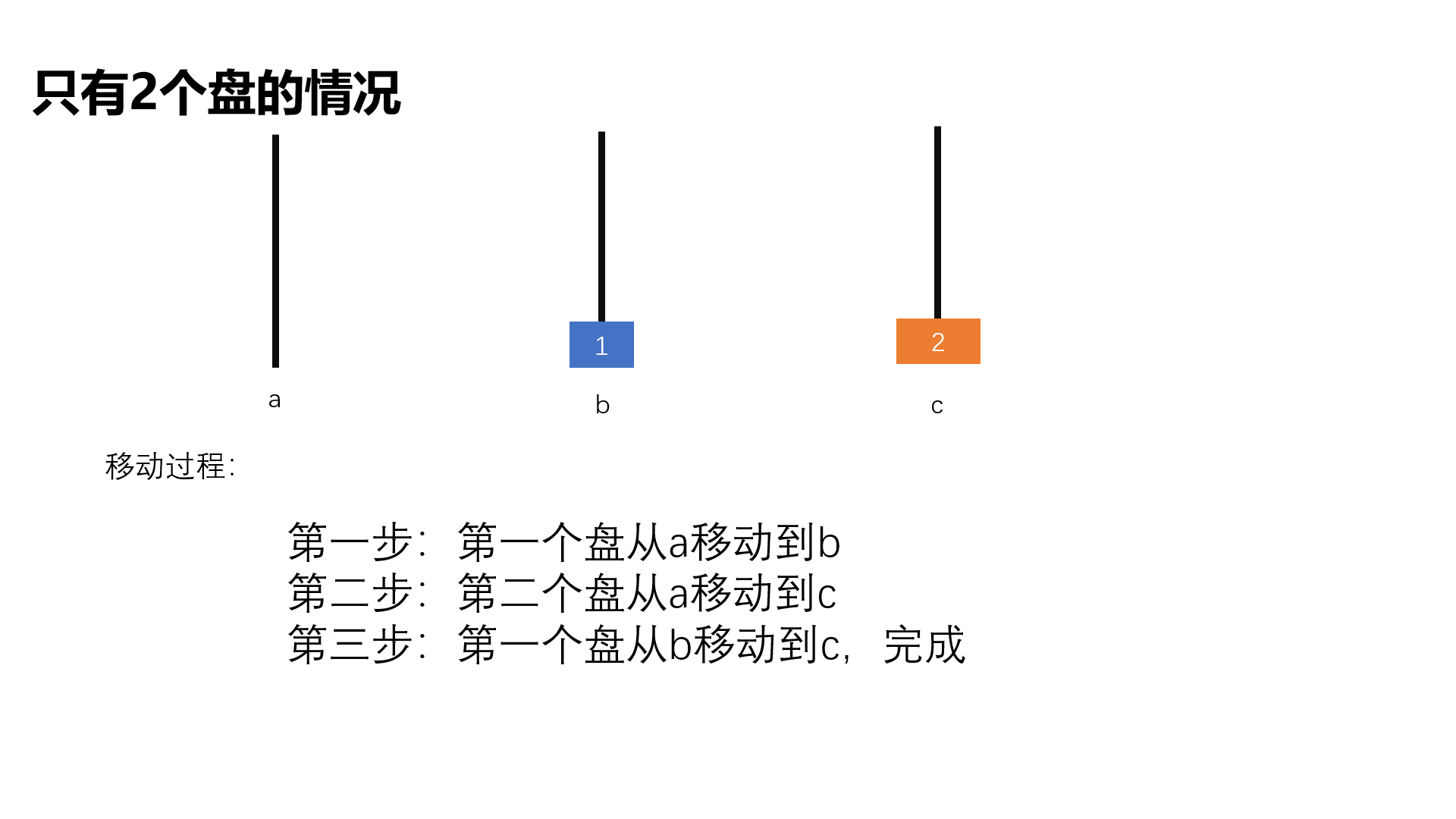
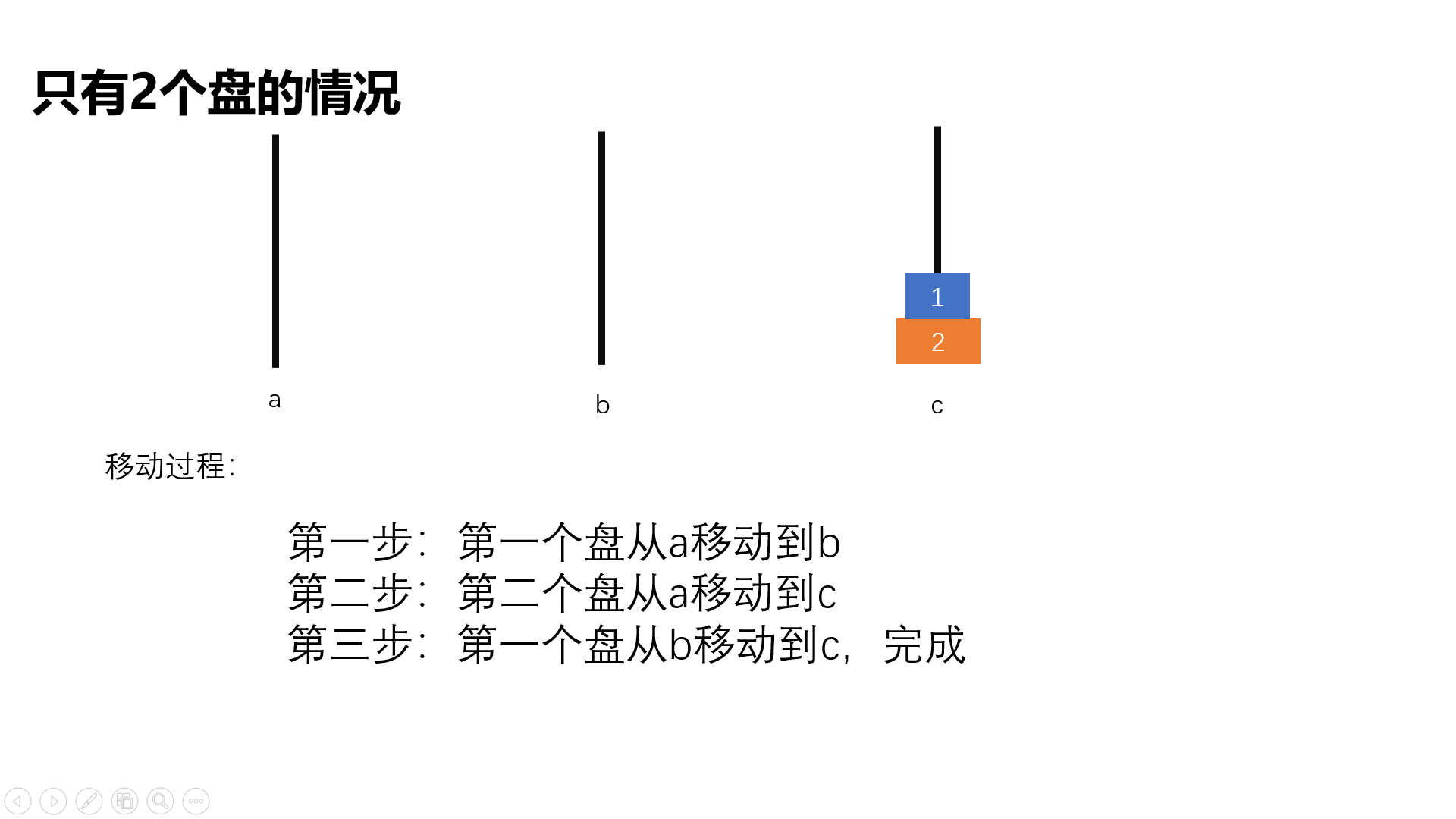
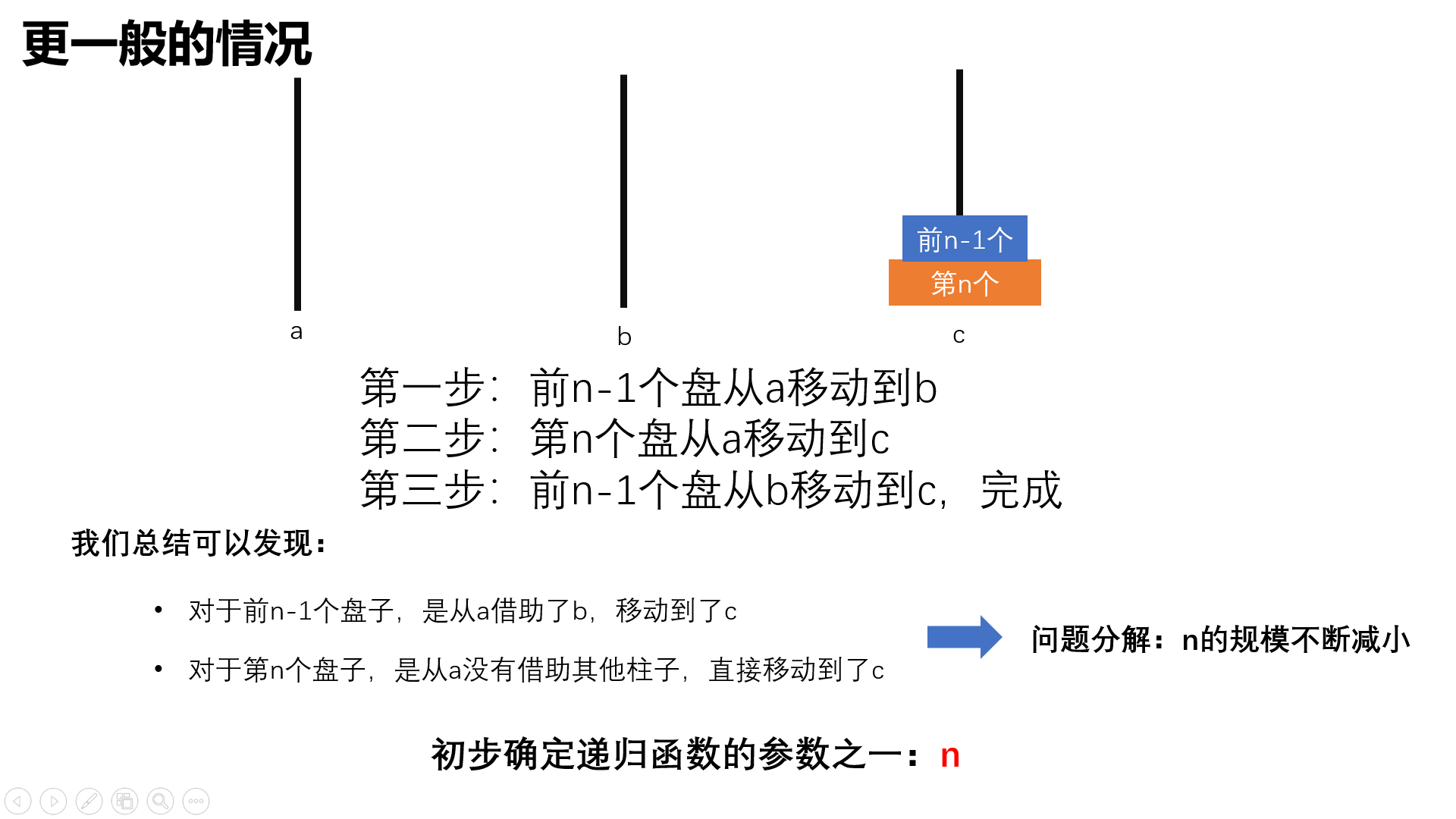
具体实现：
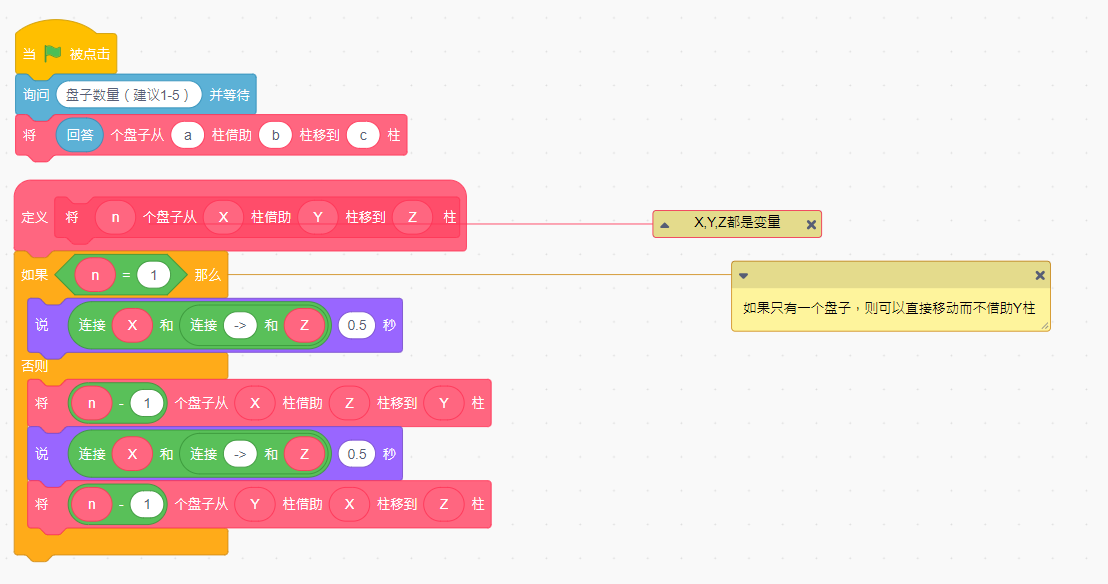
怎么样，是不是感觉递归很奇妙呢？
还等什么，快快尝试一下用递归吧！（装逼神器）
我们下节课见(预计下次会讲解如何在递归中使用局部变量和深度优先遍历,当然可能咕咕)
我是图小贝，点个赞吧~~~