友情提示：380元/半年，儿童学编程，就上码丁实验室。
题目：现有10个盒子，分别装有33、36、37、40、42、46、50、53、58和60个小球。甲先取走了两盒，其他各盒被乙、丙和丁所取走。已知乙取的球数是丁的3倍，丙取的球数是丁的4倍，那么甲取走的两盒中分别装有多少小球？
数学解法：设丁取走的小球数为1份，则乙、丙、丁三人共取走了3+4+1=8份。即它们的和可以被8整除。
利用余数的性质，将上述10个数字分别对8求余，有：
|
33 |
36 |
37 |
40 |
42 |
46 |
50 |
53 |
58 |
60 |
|
1 |
4 |
5 |
0 |
2 |
6 |
2 |
5 |
2 |
4 |
现在问题转化为：去掉哪两个数字，使得余数的和为0。
对上述余数求和，得
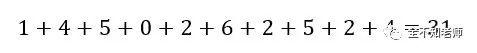
比31小，最接近8的倍数是24。31-24=7，即需要去掉的两个数字，它们的余数和为7。
上述表中没有3，所以只有1+6和2+5两种组合。
下面还需要判断能否取到：以组合1+6为例，对应的数字是33和46。去掉33和46以后，剩下的小球总数为：
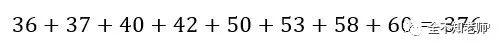
而376÷8=47。在给定的封装小盒里，没有47这个数字。因此，去掉组合33和46，实际上行不通。
排除了1+6的组合后，只有2+5组合。但是余数中有三个2和两个5，共有3×2=6种可能。
对于每一种可能，都要计算剩下八个数字的和以及被8除的商，计算量相当大。因此，这其实是一道编程题。
编程解法：根据上面的思路，可以整理出算法如下：
l将这10个数字存放在一维数组list中；
l计算它们的和total；
l取第i个数字，i从1循环到9；
l将数组中第i个元素记录为“剔除数字1”(kick1)；
n取第j个数字，j从i+1循环到10-i；
n将数组中第j个元素记录为“剔除数字2”(kick2)；
u计算剩余元素的和left，等于总和total减去kick1和kick2；
u判断left是否是8的倍数，如果是：
l计算left除以8的商unit
l判断unit是否在数组list中，如果是：
n答案的数量+1
n输出该答案
主程序部分如下：
其中的关键点是循环变量i和j的执行次数。
对于第一个需要剔除的数字，只要从1循环到9就好。如果取到10，第二个数字的下标就会变为11，出现“下标越界”的错误。
对于第二个需要剔除的数字，很显然应当从第i+1开始取值。然后对后面的数字轮流取值，前面的就不需要了。否则就会产生重复，因为无论取走33和36，还是36和33都是一样的。这样j的循环终值就是10-i。
“判断丁能否取到”部分的程序如下：
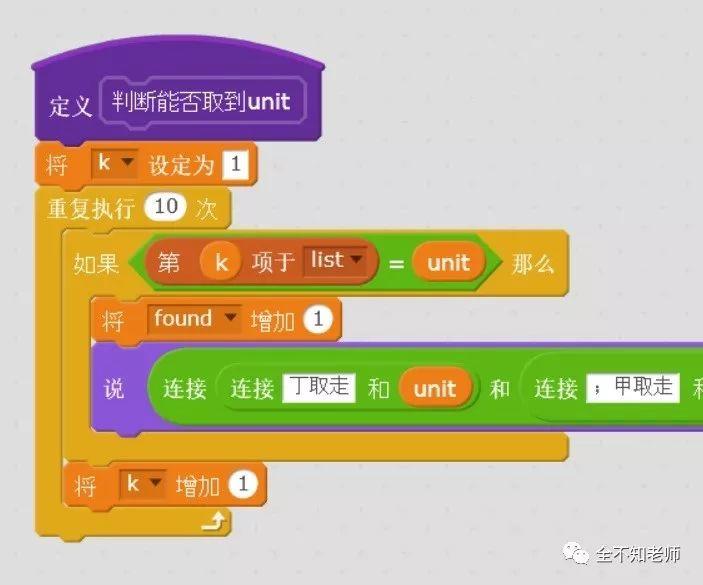
最后的结果为：
即只有一个解，甲取走37和50。丁取走46。
后记：这个题目如果作为编程题，运算量太小。如果将小球装盒的数目增加到100个，人数增加到10人。从第二个人开始，依次取走最后一个人的3倍、5倍、7倍等数量的小球。最后求第一个人应取走那几盒，就是一个标准的编程题目了。
始发于微信公众号：
全不知老师