友情提示：380元/半年，儿童学编程，就上码丁实验室。
问题描述：
棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上C点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示，A点(0, 0)、B点(n, m)(n, m为不超过20的整数)，同样马的位置坐标是需要给出的。
现在要求你计算出卒从A点能够到达B点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。
输入格式：
一行四个数据，分别表示B点坐标和马的坐标。
输出格式：
一个数据，表示所有的路径条数。
样例输入：
6 6 3 3
样例输出：
6
问题解析：
第一种方法，肯定想到搜索算法，利用dfs，每个点都尝试走一下，如果不能走则退回上一步换另一种走法，如果达到终点，路径加1；直到所有的点都尝试完为止。
代码如下：
#include <iostream>
using namespace std;
int n,m,p,q,visit[30][30],ans=0;
int b[2][2]={{1,0},{0,1}};
void dfs(int x,int y){
//如果到达终点，路径数加1
if(x == n && y == m){
ans++;
return;
}
//向右向下两种情况都尝试一下
for(int j = 0;j <=1;j++){
int mx = x + b[j][0];
int my = y + b[j][1];
//没有走过的点并且在棋盘内才可以走
if(visit[mx][my] == 0&&mx >=0&&mx <=n&&my >=0&&my <=m){
visit[mx][my] = 1;
dfs(mx,my);
//退回来记得将该点的标记取消
visit[mx][my] = 0;
}
}
return;
}
int main(){
cin >> n >> m >> p >> q;
//将马的控制点标记为不能走
visit[0][0]=1;
visit[p][q] = 1;
visit[p-2][q-1] = 1;
visit[p-1][q-2] = 1;
visit[p+1][q-2] = 1;
visit[p+2][q-1] = 1;
visit[p-2][q+1] = 1;
visit[p-1][q+2] = 1;
visit[p+1][q+2] = 1;
visit[p+2][q+1] = 1;
dfs(0,0);
cout << ans << endl;
return 0;
}
运行结果：
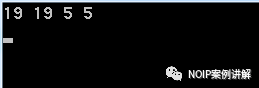
当n和m都比较小的时候，我们发现运行速度很快，运行结果没有问题，但是如果n和m稍微大一点，程序就处于超时状态。因为搜索的本质还是递归，消耗时间长，效率不高。这时我们换一个思路，用空间代替时间，使用dp算法来解决。
因为卒行走的规则只能向左或者向右，所以到达（i,j）这个点的路径数等于到达其上边点的路径数与到达其左边点的路径数之和。
状态转移方程：dp[i][j] = dp[i-1][j]+dp[i][j-1];
在使用dp算法时要考虑状态转移方程中的下标，如果从0开始，求第一行和第一列，下标将会越界。同时第一行和第一列的值比较好算，所以我们可以先把第一行和第一列的值求出来。
代码如下：
#include<iostream>
int p,q,n,m,visit[30][30];
long long dp[22][22];
using namespace std;
int main(){
cin >> n >> m >> p >> q;
//把控制点做标记
visit[p][q] = 1;
visit[p-2][q-1] = 1;
visit[p-1][q-2] = 1;
visit[p+1][q-2] = 1;
visit[p+2][q-1] = 1;
visit[p-2][q+1] = 1;
visit[p-1][q+2] = 1;
visit[p+1][q+2] = 1;
visit[p+2][q+1] = 1;
//初始化边界值
for(int i = 0;i <= m;i++){ //第一行
if(visit[0][i]){
for(int j = i;j<=m;j++){
dp[0][j]=0;//如果被马控制那么是0
}
break;
}else{
dp[0][i] =1;
}
}
for(int i = 0;i <= n;i++){ //第一列
if(visit[i][0]){
for(int j = i;j<=n;j++){
dp[j][0]=0;//如果被马控制那么是0
}
break;
}else{
dp[i][0] =1;
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
//一个点的路径来自左方与上方
dp[i][j]=dp[i-1][j]+dp[i][j-1];
//如果被马控制那么是0
if(visit[i][j]) dp[i][j]=0;
}
}
cout << dp[n][m];
return 0;
}
如果大家有更好的方法，欢迎多多交流！
转自公众号：
noip案例讲解