友情提示：380元/半年，儿童学编程，就上码丁实验室。
在编程教学中，讲到循环时，都会用积分来举例和做练习。今天我们谈谈用梯形法求定积分。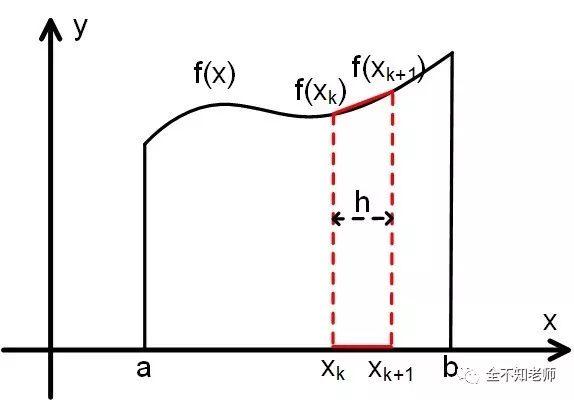
原理：设有函数f(x)，它的区间[a,b]上的定积分，等于其与X轴之间包围的面积。
将区间[a,b]分成若干等分。假定每等分的长度为h，则等分数N为：
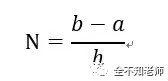
曲线与X轴之间的面积，可以看成是这N个梯形的面积之和，
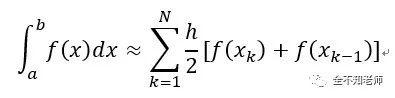
设函数在端点处的函数值为f(a)和f(b)，则有，
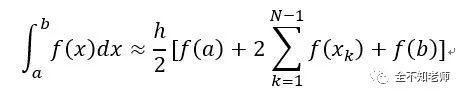
实例：计算下列函数的定积分值，
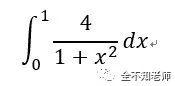
其中h = 0.002。
程序：利用Scratch编程的算法部分如下：
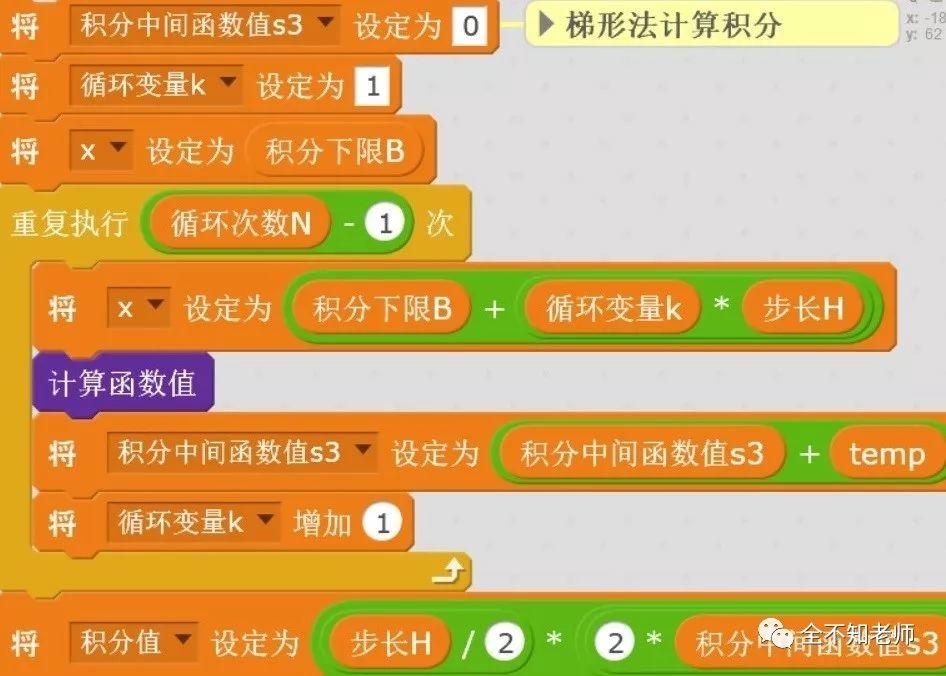
其中各变量的含义如程序所示，a为积分下限，b为积分上限，H为步长，N为积分次数。
s1为积分下限函数值，s2为积分上限函数值，s3为中间求和部分。k为循环变量，temp为中间变量。
子程序“计算函数值”的程序如下：
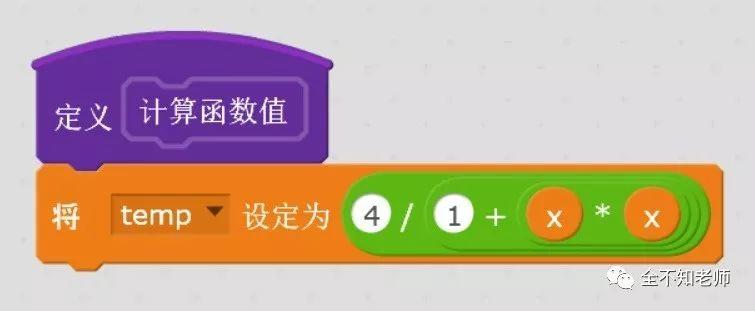
其中x是自变量，temp是计算的函数值。
由于Scratch不支持参数传递，所以通过全局变量进行传值。
计算结果如图所示：
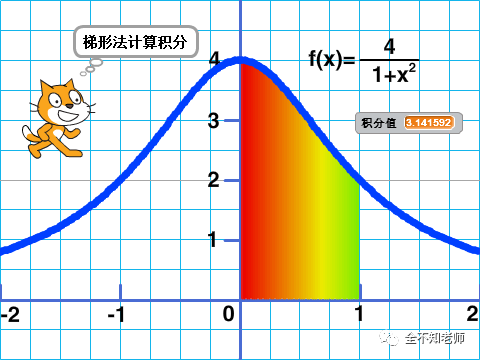
后记：发现没有，计算结果等于圆周率π。哇！怎么这么奇妙？原来该积分可以得出原函数：
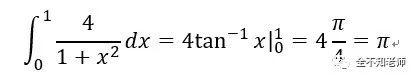
这是另外一种可以精确求出圆周率Pi的方式。
另外，为了让程序更富有表现力，生成了函数f(x)的图像，并配上了坐标轴和刻度，以及Scratch那只无处不在的小猫咪。
始发于微信公众号：
全不知老师