友情提示：380元/半年，儿童学编程，就上码丁实验室。
今天我们来介绍一下“李萨如图形”。所谓的李萨如图形(Lissajous Figure)，是指两个互相垂直的简谐振动合成的封闭图形。
背景知识：何谓“简谐振动”，有点类似荡秋千、钟表的摆动或者是弹簧“Biu”的一声弹起来。
此物理现象的数学表达式为：
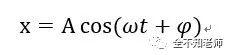
其中A为振幅，ω(读作omiga)为角频率，ψ(读作psai)为初始相位。
由于正弦函数和余弦函数相差90度，所以这就是为什么正弦函数如此重要的一个原因啦。初中数学中关于三角函数部分的知识，主要是学习正弦函数。高中数学部分也是紧紧围绕正弦函数展开的，它是核心中的核心。
当空间上互相垂直的两个正弦信号进行叠加时，如果他们的角频率之比以及相位差满足特定条件，可以形成稳定的图形，即李萨如图形。在工程上，常用这个简便方法来确定信号的角频率和初始相位。
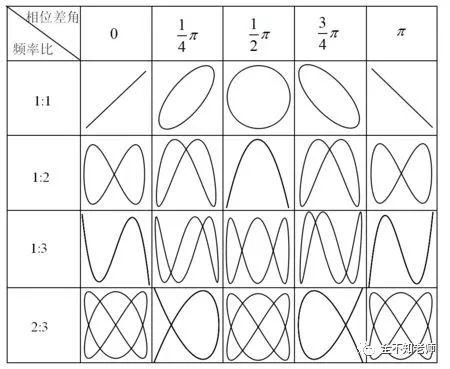
下面我们用程序来演示一下吧。
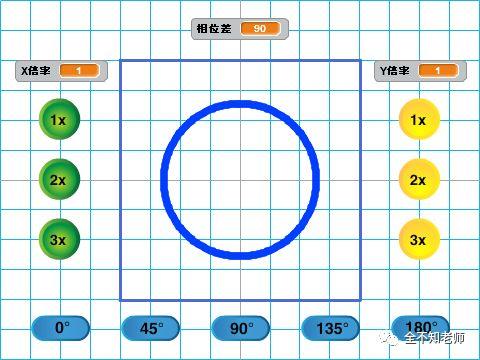
功能介绍：首先看下片头，这是X通道和Y通道的比值为1：1，相位差为90度时的李萨如图形。
对，它就是圆。这是绘制圆的一种方法。
屏幕左侧的按钮可以调节X通道输入信号的角频率，按下“X”键可以绘制X通道的信号。
屏幕右侧的按钮可以调节Y通道输入信号的角频率，按下“Y”键可以绘制Y通道的信号。
屏幕底部的按钮可以调节X通道和Y通道信号之间的相位差。按下“O”键可以绘制合成的李萨如图形。这里展示的是1：1时候的情形。
下面是X通道与Y通道比值为1：2时的情形：
X通道与Y通道比值为1：3时的情形：
X通道与Y通道比值为2：3时的情形：
(一次只能上传3个小视频，而且每个文件有大小限制。。。)
哈哈，像不像一个示波器啊。
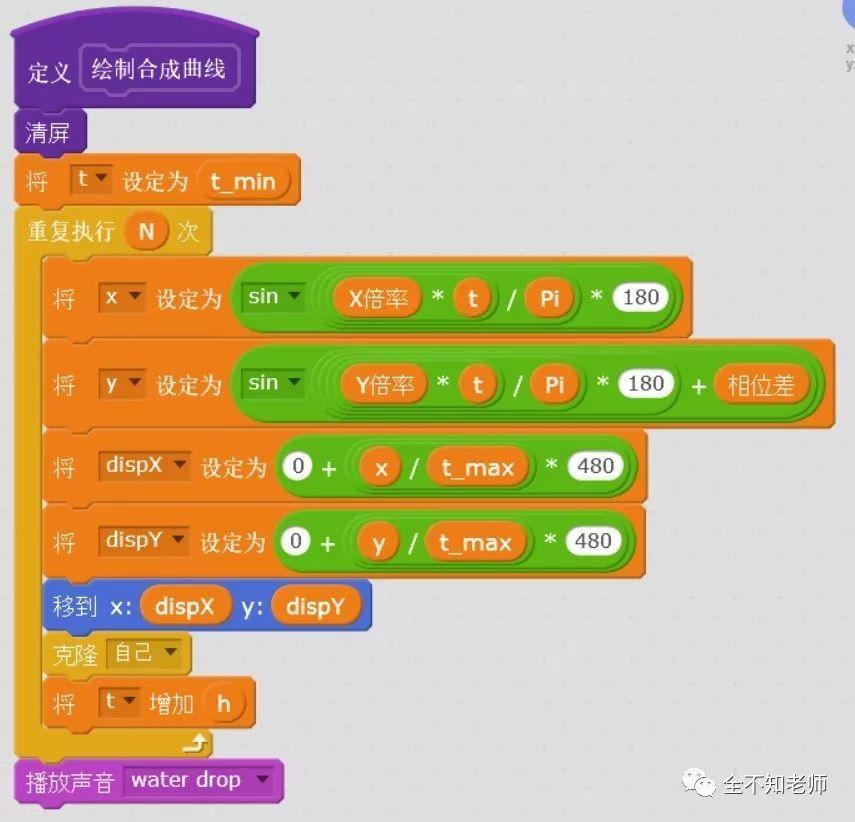
程序实现：小小“示波器”的功能很强大，下面只介绍其中核心部分，即李萨如图形的生成算法。如图所示：
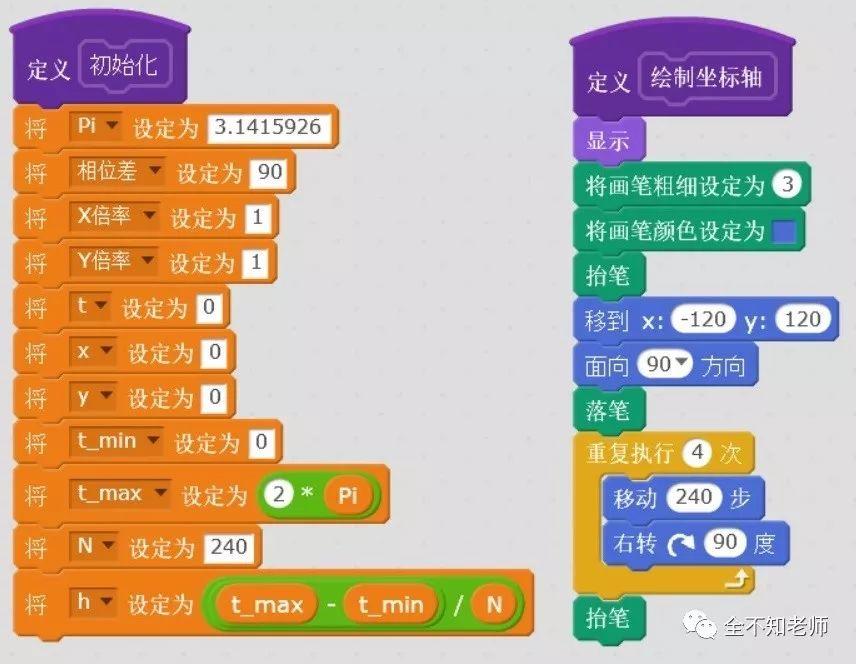
其中x对应横坐标，y对应纵坐标。t是参数变量，t_min是参数t的下限，t_max是参数t的上限，这里对应[0,2π]。N为循环次数，h为循环步长，
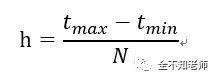
在初始化时，相位差设为90度，X倍率设为1，Y倍率也设为1。
要点一：缺省值。由于在本程序中，相位差对应0度、45度、90度、135度和180度五个值。X倍率和Y倍率分别对应1、2和3。程序运行初始赋予它们的值，称为缺省值。这是一个常用的编程技巧，使得开始不需要输入数值就可以运行。
要点二：子程序。无论“初始化”还是“绘制坐标轴”部分，都采用Scratch称为“积木”的方式编写。这种编程技巧通常被称为子程序，主要用于某段程序需要多次运行的场合。
该程序对应的参数方程为：
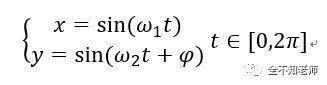
要点三：角度和弧度的转化。在三角函数的讨论中，通常采用弧度制。360度相当于旋转一周，因此对应2π。即有下列换算关系：
在Scratch中，三角函数使用角度制。为了便于计算机绘图，需要转换为弧度制。
X倍率为1时的图像。
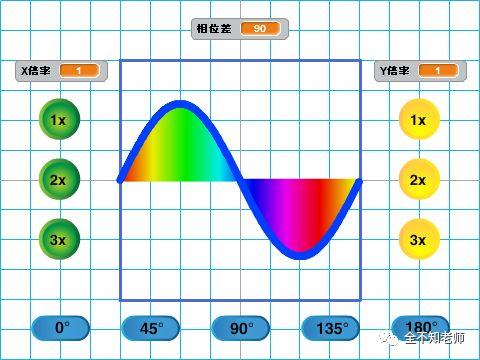
Y倍率为1时的图像。
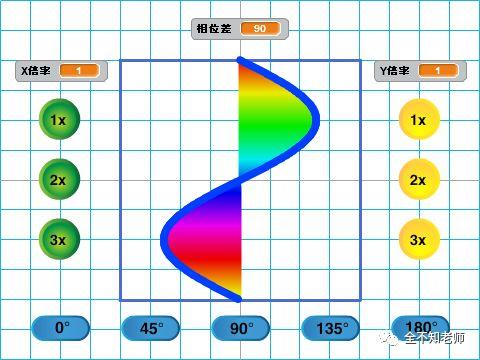
相位差为90度时，它们合成的李萨如图形为：
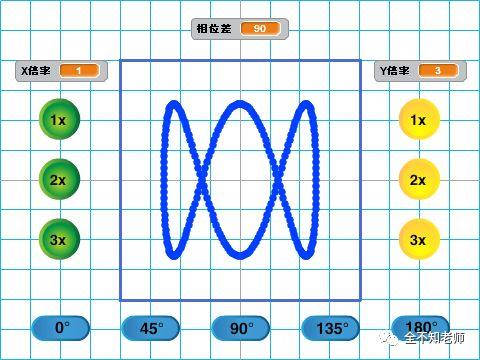
下图时X倍率为1，Y倍率为3，相位差为90度时的图形。
后记：简谐振动的标准形式是写成余弦函数的形式。有的同学不禁要问，既然大家对正弦函数学习和了解的更多，为什么用不采用正弦函数的形式呢？原因如下：
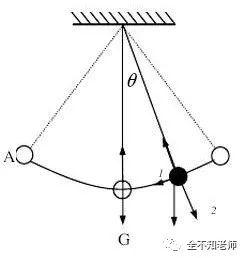
以单摆为例，将单摆拉开一个角度，然后松手，单摆就开始进行摆动。起始位置对应于振幅最大点，速度为0。而当单摆摆置最低点时，振幅为0，速度最大。这正对应了余弦函数的图像，而不是正弦函数。
始发于微信公众号：
全不知老师