Scratch教程：坐标旋转“华尔兹”

在上一篇中，我们介绍了坐标变换的基本方法，并使用自定义积木完成了坐标变换。使用坐标变换，我们得到了放大缩小、平移、镜像及倾斜的效果。

这一次，我们研究一下旋转的坐标变换。

变换的意义

　　知道一个点的X，Y坐标，围绕中心原点旋转一定的角度，看这个点会移动到哪个位置上。因为涉及到旋转，就要涉及到三角函数的使用。

二维坐标下，旋转坐标变换使用矩阵的方式写出来是这样的。

   

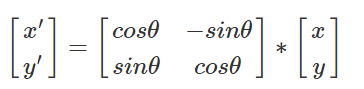
分解后可以写成下面的形式：

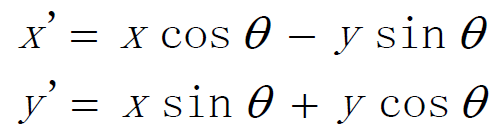
公式中的θ就是需要旋转的角度，x,y是原来的坐标，x’,y’是变换后的坐标。

 

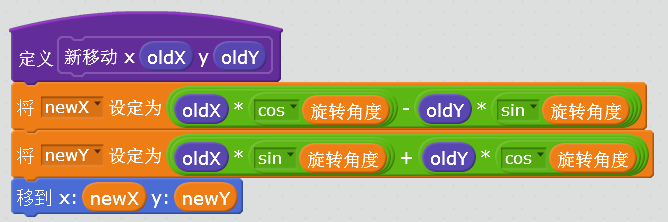
我们仍然以上次的房子为例，试着把它旋转45度。则积木变化为下面这样，可以看到这块积木将旧的坐标根据旋转的角度变化为了新的坐标。

得到的效果是这样

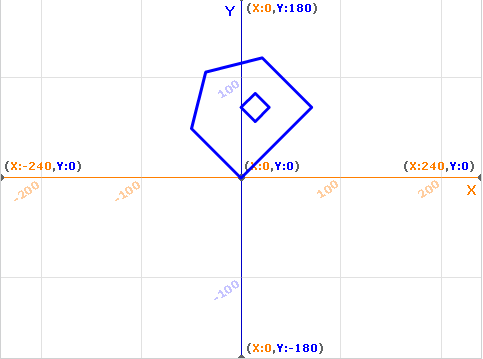
可以看到房子沿逆时针方向转动了45度。

基于这个角度的变换，进行一点小小的变化，就可以得到很有趣的效果。

 

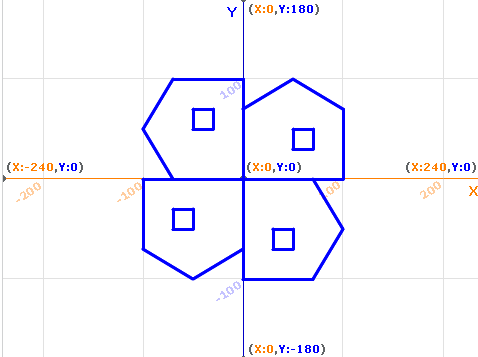
下面我们再使用这个方法，做一个椭圆的坐标变换。

 

大家知道，使用参数方程可以表示出椭圆。

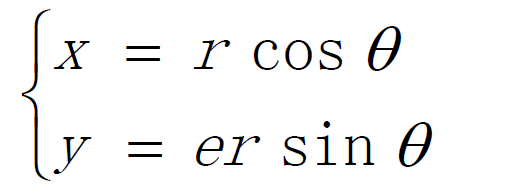
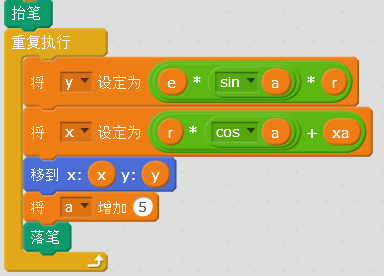
其中e为Y轴与X轴的比率，a表示角度，r表示半径。xa是椭圆中心点的位置。这样得到如下的结果：

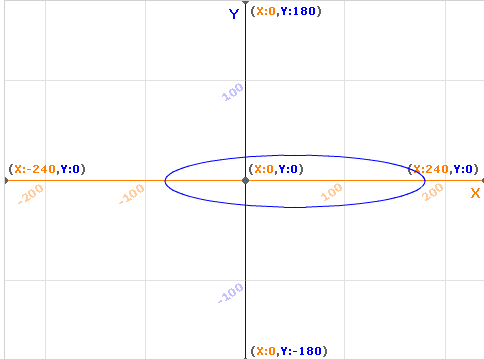
如果我们想绘制转动的曲线，就需要对坐标进行变换。

我们可以增加一个旋转的角度，对于椭圆上的每一点进行变换，就可以得到每个点的新坐标。

将a0设置为旋转的角度为45度。

设置上面的sina及cosa变量是为了加快计算的速度，这样就不需要每次计算点时重新计算三角函数了。

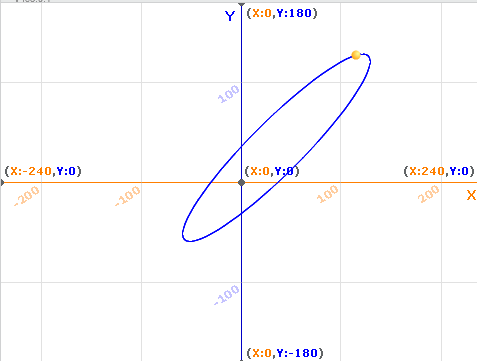
可以看到，通过坐标变换，得到了一个倾斜的椭圆。

 再设置几个克隆体，就能够演示出几个物体围绕中心运行的路线了。

 

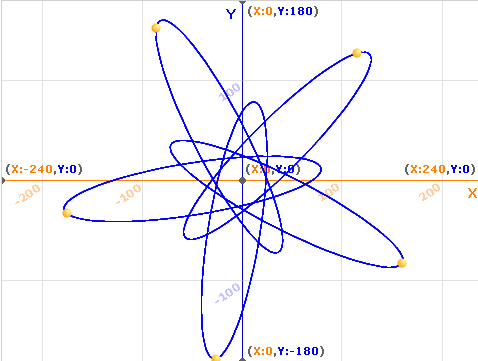
上面提到的所有变换，都可以叠加起来使用，大家可以自己试验。

大家会发现：

在叠加多个变换时，变换的次序不一样，则得到的结果也不一样。

也就是先平移再转动与先转动再平移的效果是不同的。

 

 

总结

 

结论：

1 　使用坐标变换，可以得到旋转的效果。

2 　坐标变换的数学基础是矩阵计算，有兴趣的同学可以自己学习研究一下。

3 　不同变换的组合效果与变换的先后次序是有关的。