Scratch教程：角色的运动齐步走！

Scratch中提供了多个积木控制角色的运动、旋转等。但很多时候需要同时移动、转动及进行大小及颜色等特效的渐变。如何协调这些参数的变化，使得角色的运动、转动及变化步调一致呢？

例子：

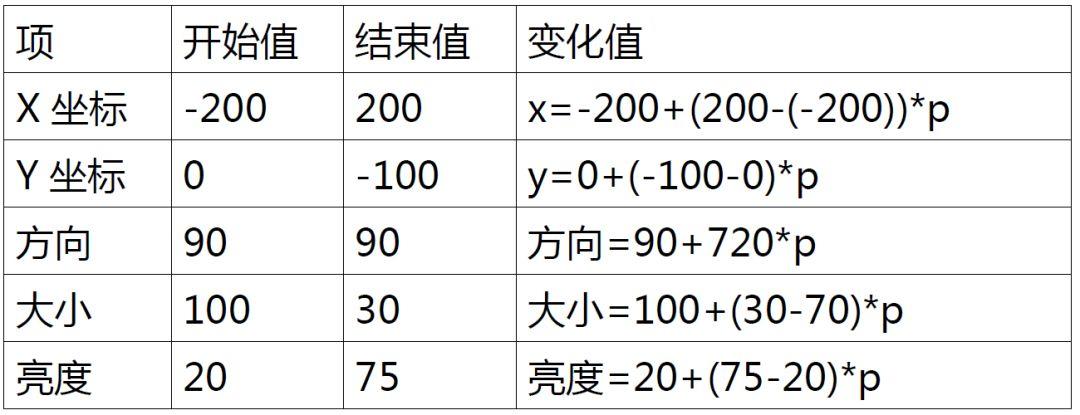
　　要求角色在5秒内，从(-200，0)运行到(200，-100)，在这个过程中顺时针旋转2圈，大小从100变成30，角色的亮度从20变到75。

程序中有在一定时间内移动到某一坐标的积木，可以用于平滑移动，但对于转动、大小和特效，就没有类似的积木了。

怎么办呢？

求　解

 

我们可以确定一定的时间步长，使用循环的方式，通过自己变化变量的值，控制角色的移动、转动及其它效果的变化。

以1秒为时间步长（共5步），可以列出下表来分析问题：

                           

程序是这样的

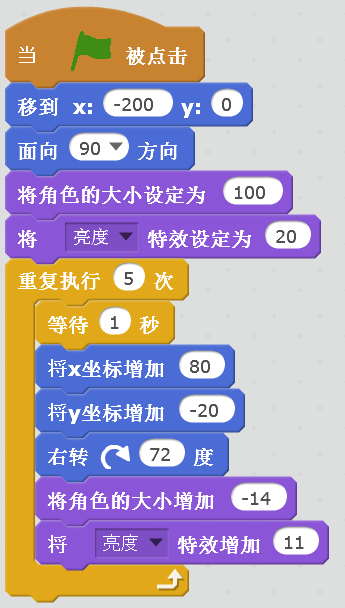
效果如下

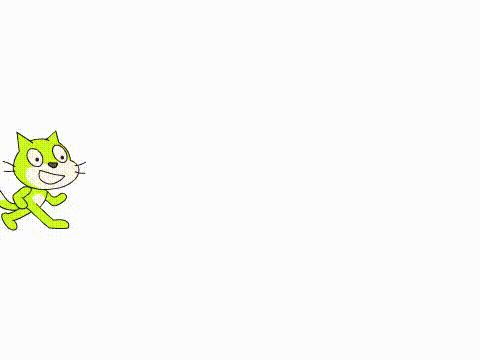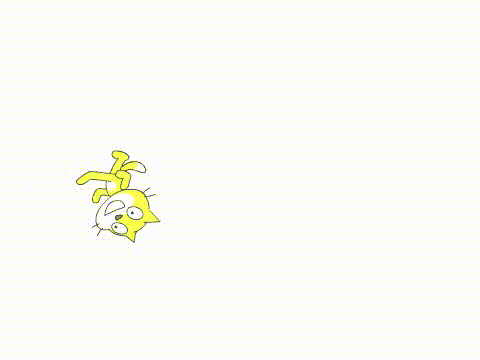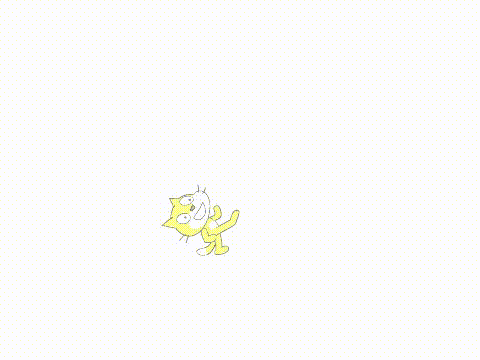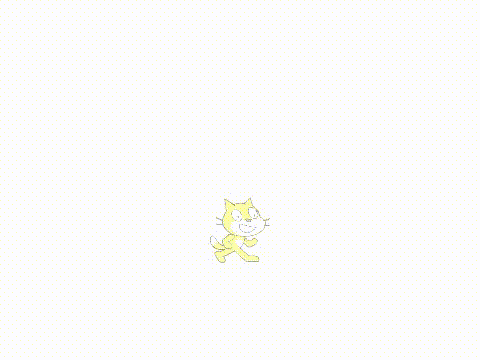
可以看到，现在的程序由于每次变化1秒，运动不够平滑。

如何使变化平滑呢？

直观的办法当然是减小时间步长。但使用这种方式存在如下的问题：

1　改变时间步数时，比如将整个变化分为10步，每次时间步长为0.5秒，就需要重新计算每步的变化值。

2　如果改变了参数的初值或终值，还需要重新计算每步计算值。

3　每次开始时，都需要使用积木为坐标、转动、大小及特效等设置初始值。

4 　如果除出来的结果带很多位小数，在保留的小数位不够时，就会造成最后的结果不准确。

 

 

如何做呢？

这里作者提出一种基于插值的解决方案。

从数学上说，这些参数值的变化可以认为是线性插值的问题，也就是在已知端点时，使用直线描述变量随时间的变化的问题。如果绘制各参数随时间的变化，应该像下图这样。

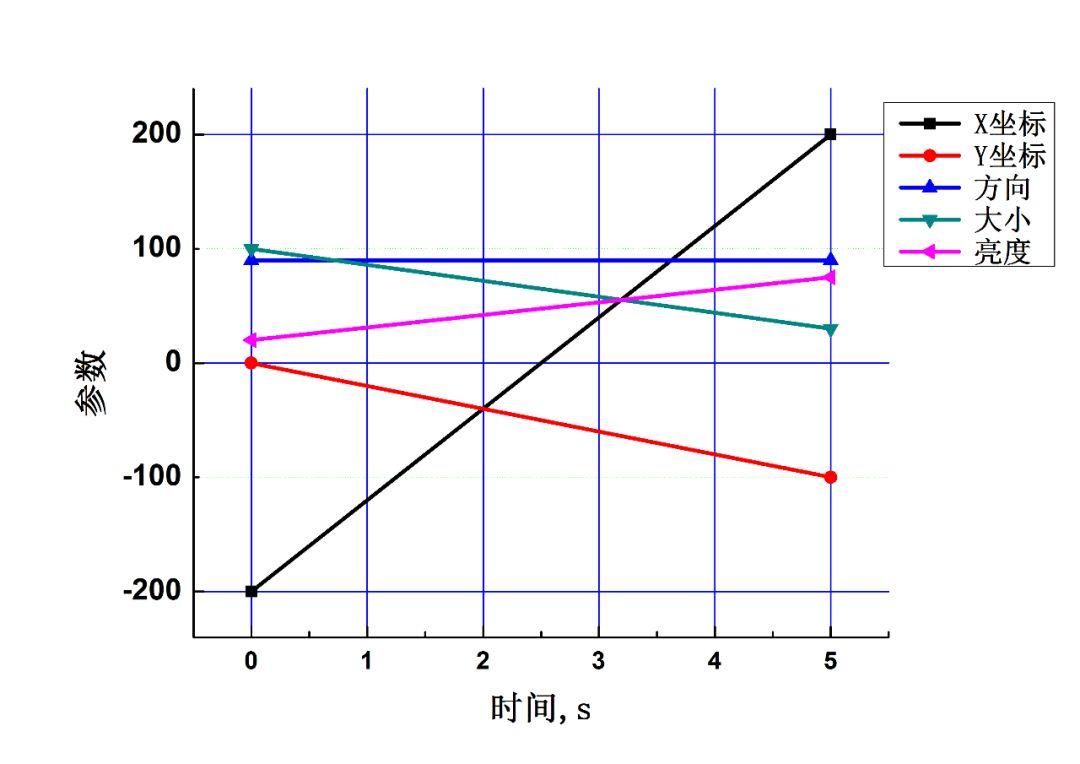
对于我们的问题，在值的变化范围内，一般情况下变化是与时间成正比的。从数学上说，两个变量之间是线性关系。每个变量都是从区间的开始变化到区间的结束。这样，我们可以用一个变量p来表示一个量在区间中的位置。这个变量的范围是0到1，p=0时对应开始值，p=1的时对应结束值。

如下面的公式：

 

所有的参数都可以用这个方法进行处理。那么，这个p又是从那里来的呢。p可以根据当前的时间与总时间的比值来进行计算。即

为什么使用0-1呢，实际上这是数学中的归一化思路，便于将范围不同的数字放到同样的范围(0到1)内进行比较和处理。

这样，参数就可以这样进行计算：

根据这个算法，程序可以这样写：

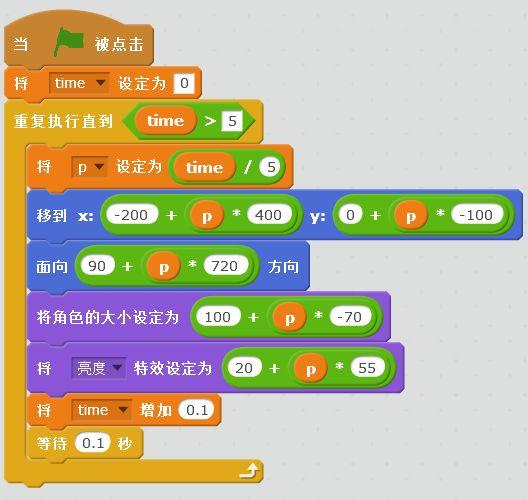
如果如下

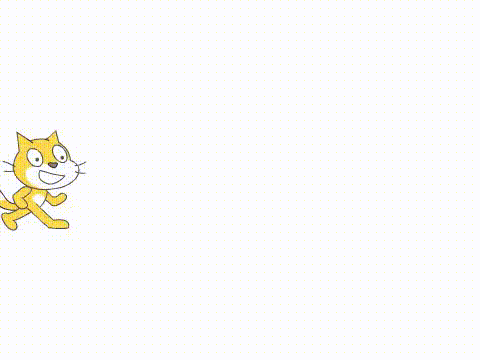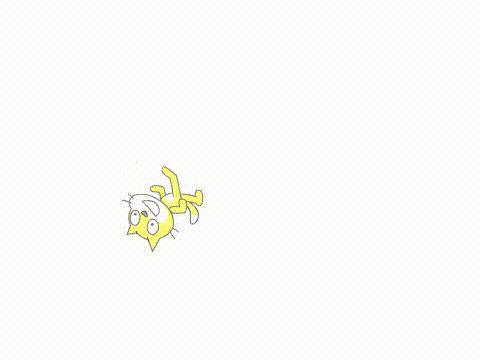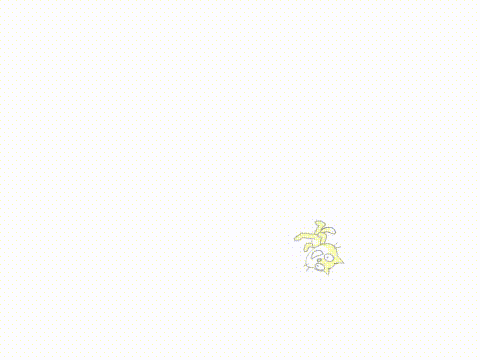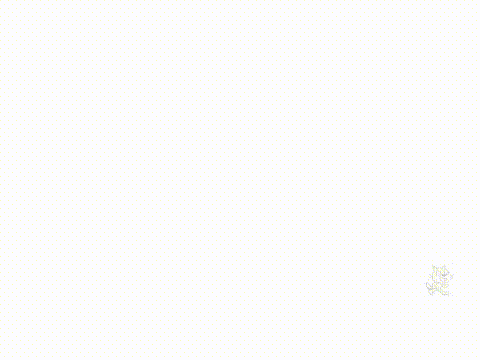
如果根据p值的变化，应用三角函数进行处理，就会很容易地得到更加有趣的变化。只需要将上例修改一句                             

并在后面增加印章积木，就能得到这个效果：

 

优点

 

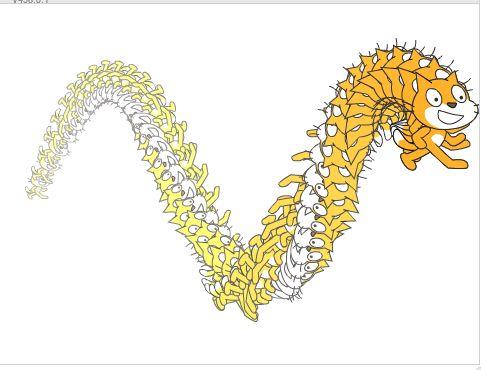
1　改变时间的步长十分方便，便于调节步长及平滑效果。

2　不需要计算步长，只需要给出开始值及结束与开始的差值即可，便于调整。

3 　各点的公式形式一致，便于检查错误及修改。

4 　可以外延，虽然我们推导时p的范围是0到1，但实际上超过范围也是可以的，相当于对原来变化的一个外延。

 

总结

1 　使用数学中的线性插值及点斜式直线方程，协调各个变量的同时变化。2 　基于这种方式的程序简单易懂，便于调整和修改。

3　这种方法中的归一化，也是数据处理中的一个常用方式。