Scratch教程：谁算的快？

多项式是由若干个单项式相加组成的代数式，它在数学中十分重要，在拟合、插值、数值积分及微分中有很多的应用。

多项式的形式如下图所示，其中的n称为多项式的次数。

我们常常需要在已知x的情况下计算出y。如果直接分项进行计算，需要计算x的多次方，会消耗比较多的计算时间。

以下面的多项式为例：

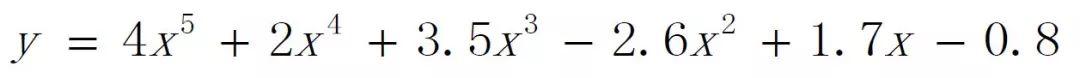
如果直接进行计算，需要进行5+4+3+2+1=15次乘法和5次加法。

 

如何能节约计算时间呢？

算法研究

这就需要使用秦九韶研究的算法了

﹀

﹀

﹀

 

秦九韶

秦九韶（约公元1202年－1261年），字道古，南宋末年人，出生于鲁郡（今山东曲阜一带人）。秦九韶算法是他提出的一种多项式简化算法。在西方被称作霍纳算法。

秦九韶算法是一种将一元n次多项式的求值问题转化为n个一次式的算法。其大大简化了计算过程，即使在现代，利用计算机解决多项式的求值问题时，秦九韶算法依然是最优的算法。

 

一般地，一元n次多项式的求值需要经过n*(n+1)/2次乘法和n次加法，而秦九韶算法只需要n次乘法和n次加法。在计算时，大大简化了运算过程。算法的原理如下：

把一个n次多项式

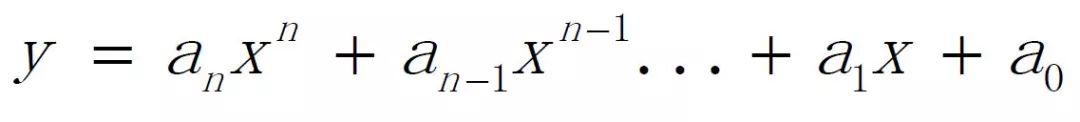
改写成如下形式：

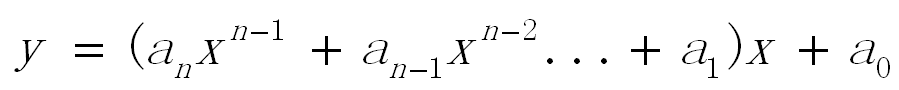
多项式的值时，首先计算最内层括号内一次多项式的值，然后由内向外逐层计算一次多项式的值，即

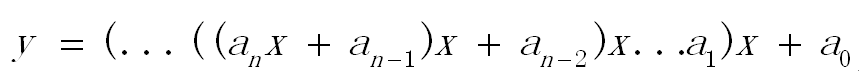
这样，求n次多项式f(x)的值就转化为求n个一次多项式的值。

 

这个算法也是教育部新编的教学大纲，《普通高中信息技术课程标准（2017版）》中要求的内容。

下面，我们看看在Scratch中如何实现这个算法，并对两种不同计算方法使用的时间进行比较。

我们对下面的多项式进行计算。

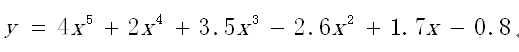
如何来记录使用的时间呢？

可以使用计时器，在开始运算时，将计时器设置为0。在结束计算时，取得计时器的值，就得到了计算所使用的时间。

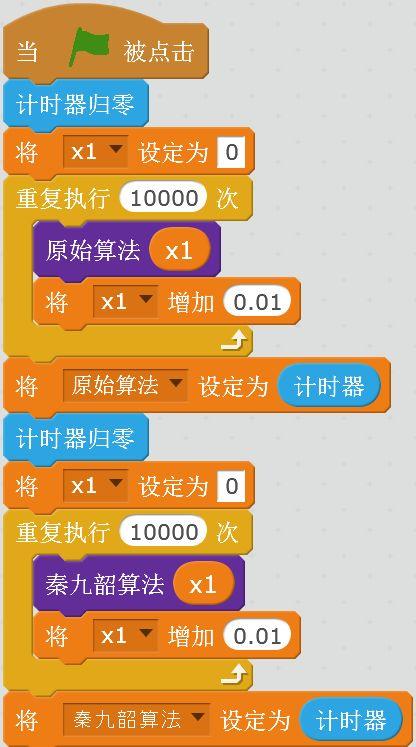
下面是主程序，为了能够比较准确地统计使用的时间，让每种算法分别运行10000次，记录总的时间。

 

原始的算法子程序如下：

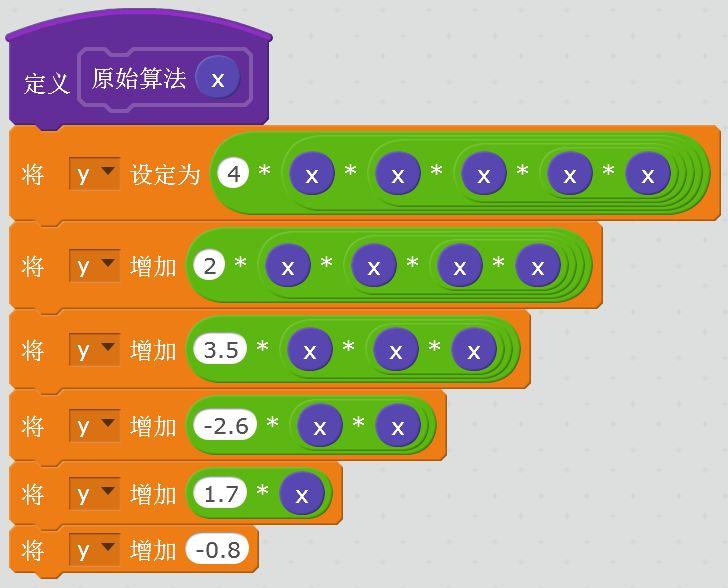
按照上面的算法描述，将方程修改为如下的形式：

         

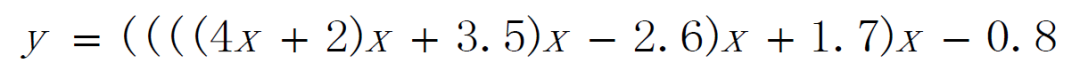
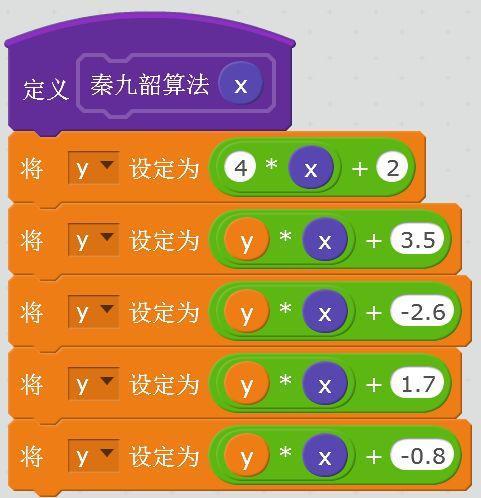
            则秦九韶算法子程序如下。

运行后，可以得到两个算法所消耗的时间。（由于计算机的配置不同及操作系统的不同，计时结果可能不同）

可以看出，使用秦九韶算法，不但能够减少计算量及计算时间，而且程序比较简洁。

 

结论

1    对于同样的一个问题，由于使用了不同的算法，开发出的程序复杂程度不同，而且运算时间也不相同。

2    在不影响精度的情况下，秦九韶算法可以极大地节省计算量和计算时间。

3    虽然计算机的运算速度在不断地提高，但对于算法改进的研究是永恒的主题。

4     在程序设计中，可以使用计时器的方式，对于需要计算的时间进行测量和分析。