码丁实验室,一站式儿童编程学习产品,寻地方代理合作共赢,微信联系:leon121393608。
用Scratch巧解数学题
——求最大公因数

问题:求两个非零自然数a和b的最大公因数。比如,求12和15的最大公因数。
怎么求两个非零自然数的最大公因数?一般采用列举法或者短除法。但是,如果两个数较大,采用这两种方法就不太容易了。比如,36963与59570的最大公因数是多少?用列举法或者短除法基本上求不出来。即便数字再小一些,比如423和327的最大公因数是多少?要求出它们的最大公因数也不是一件容易的事!
求最大公因数还有其他方法吗?当然有!辗转相除法呀。虽然辗转相除法在目前的小学教材中没有介绍,但是辗转相除法却是已知的最古老的算法。其可追溯到3000年前,由数学之父欧几里得提出来的,所以又名欧几里得算法。这种算法,在我们中国可以追溯到东汉出现的《九章算术》。
Scrach编程一般面向的是小学生呀,小学教材都没有介绍辗转相除法!还有其他方法吗?好像没有。等等,让我再想想。间接法!这真是,山重水复疑无路,柳暗花明又一村!当我们通过直接法没有办法解决问题时,我们不妨换一个思路,不要老想着怎么直接去求最大公因数!
我们知道:两个非零自然数a和b的乘积,等于它们的最大公因数和最小公倍数的乘积。写成公式就是:
a×b = (a,b)×[a,b]
比如,12×15 = 3×60
既然最大公因数不好求,那我们想办法求出最小公倍数不也就求出了最大公因数吗?写成公式就是:
(a,b)= a×b ÷ [a,b]
比如,(12,15)=12×15÷[12,15]=3
这就是间接法!其实就是一种转化的思想。
问题就转化成求两个非零自然数的最小公倍数!求两个非零自然数的最小公倍数一般采用列举法。列举法具体是这样的:先列举出第一个数的一倍数、二倍数、三倍数…;再列举第二个数的一倍数、二倍数、三倍数…,直至第一个同时在第一个数的倍数中出现的数,这个数就是两个数的最小公倍数。文字描述比较拗口,举例说明:
12的倍数:12、24、36、48、60、72…
15的倍数:15、30、45、60
60就是12和15的最小公倍数。
我们可以把列举法做一点点改变:就是用第一个数的一倍数、二倍数、三倍数…去除以第二个数,第一个能除尽的倍数,就是这两个数的最小公倍数。12的倍数中60是第一个能被15整除的数,因此60就是12和15的最小公倍数。
有了具体的算法,就很容易通过编程让计算机来帮助我们计算了!为了让程序更加清晰明了,我们可以把求最小公倍数写成一个过程,主程序去调用这个过程。首先还是根据算法画出求最小公倍数过程的实现流程图。
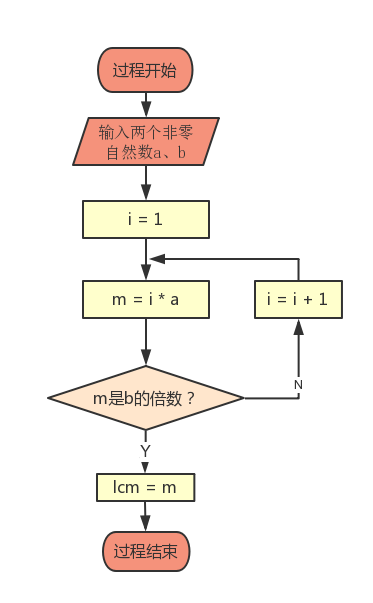
有了流程图,编写代码就很简单了。流程图就是编程的施工图。学习编程,画流程图是基本功。一定要养成无流程图不写代码的好习惯!流程图本身就是编程思路的体现,通过画流程图也可以进一步整理我们的思路。

主程序通过人机交互输入两个非零自然数,然后调用这个过程就可以了。直接上代码!
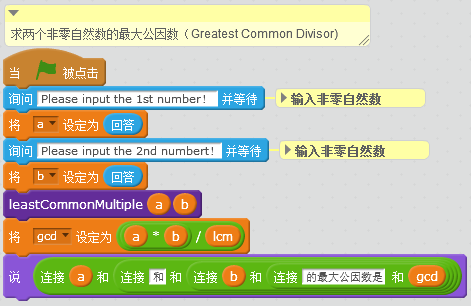
程序写好后,还要调试,看看功能是否正常。运行程序,按照提示依次输入两个非零自然数,36963和59570,结果很快算出来了,“36963和59570最大公因数是37”。秒杀!
计算机是不是很强大呀!但前提是你要会编程呀!只有会编程,你才能让计算机替你解决问题呀!别担心,编程其实也没有想象那么难!只要你愿意学。
Scratch虽然是专门为少儿设计的编程语言,但其功能还是非常强大的,不仅可以创建动画、游戏和故事书,还可以用来求解数学题,实现一些数学算法。学过Scratch后,将来再学习其他高级程序设计语言,理解起来也会更加顺畅,更加容易!

