码丁实验室,一站式儿童编程学习产品,寻地方代理合作共赢,微信联系:leon121393608。
我们将使用程序求解圆周率,通过这个实例来感受计算机程序给人类带来的计算能力的巨大提升,这种便利对以前的数学家、科学家等需要大量计算的人群来说是无法想象的。

在编程之前,让我们一起回顾什么是圆周率,以及了解圆周率计算方法“割圆术”。
圆周率与割圆术
什么是圆周率?
π is commonly defined as the ratio of a circle’s circumference C to its diameter d.
The number π (/paɪ/) is a mathematical constant. Originally defined as the ratio of a circle’s circumference to its diameter, it now has various equivalent definitions and appears in many formulas in all areas of mathematics and physics. It is approximately equal to 3.14159. It has been represented by the Greek letter “π” since the mid-18th century, though it is also sometimes spelled out as “pi”. It is also called Archimedes’ constant.
圆周率 π 是一个数学常数,为一个圆的周长 C 和其直径 d 的比率,约等于3.1415926,它在18世纪中期之后一般用希腊字母π指代,有时也拼写为“pi”。
—— Wikipedia
如图,圆周率 = 圆的周长 ÷ 直径。
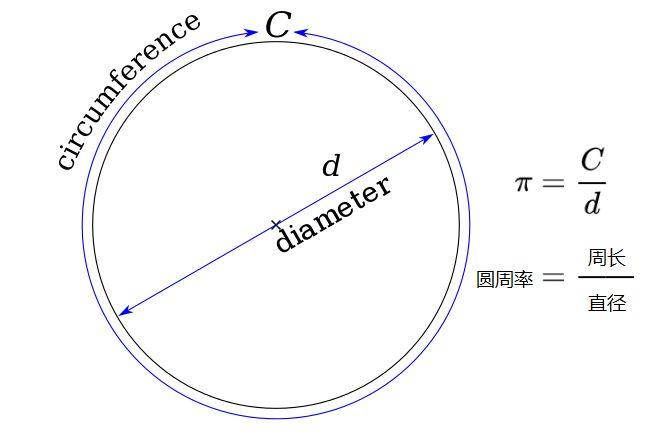
什么是割圆术?
“割圆术”是一个重要的求解圆周率的方法,三国时代的刘徽、南北朝数学家祖冲、希腊数学家阿基米德等等,都是使用割圆术完成自己最圆周率π的计算。
下面是刘徽的著作中关于割圆的描述,他算出的圆周率值是3.1416。
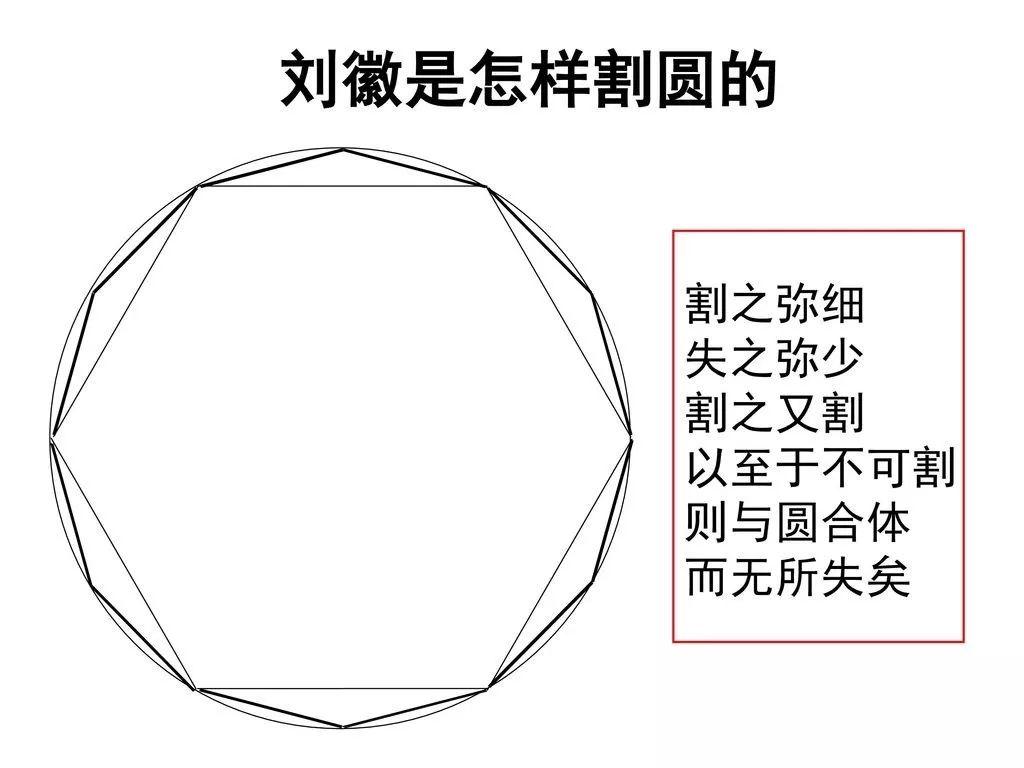
简单一点解释,割圆术就是在圆内绘制等边多边形,当多边形的边数越多时,多边形的周长与圆周越是相近,同时,多边形周长除以圆直径的值越接近某一个固定值,这个值被称作“圆周率”。
下面分别是6边形、12边形、24边形、48边形,可以看出48边形比6边形更相似于圆,有理由相信,边数继续增加后,多边形会更加近似于圆。
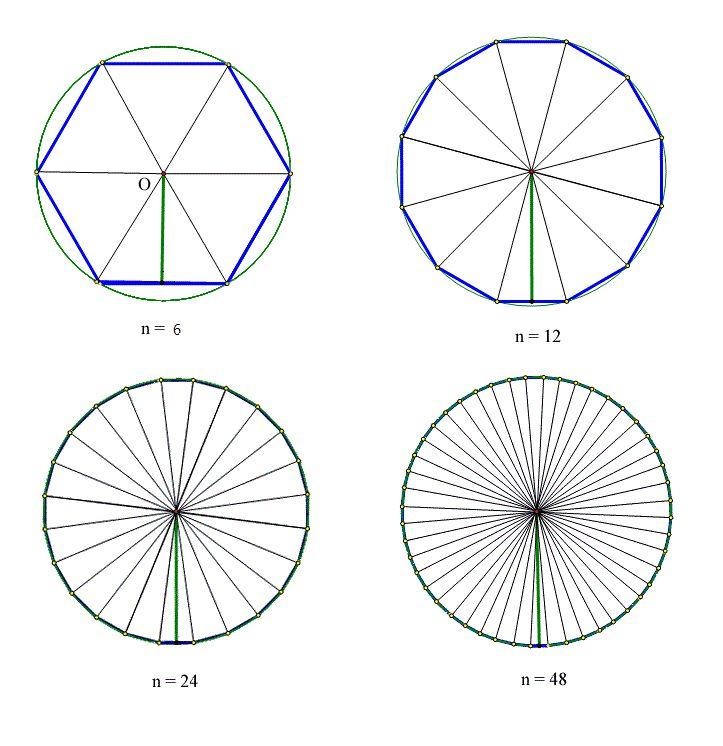
在约公元480年,祖冲之利用割圆术计算24567形的边长,得到 π ≈ 355113(现在称为密率),其数值为3.1415926~3.1415927,小数点后的前七位数都是正确值。直到一千多年后才由15世纪的阿拉伯数学家阿尔·卡西以17位有效数字打破此记录。为纪念这位伟大的中国古代数学家,有人将 π ≈ 355113 称作“祖率”。
00 算法分析
学习了割圆术,我们来思考怎样将它转化成程序语言。
首先我们要动态的画出一个圆,更准确的说,我们要画一个圆的内切多边形,通过逐步增大多边形的边数,观察多边形逐渐向圆靠拢的过程,同时,观察圆周率逐渐变得精准的过程。这个动画过程,可能需要用到圆心、半径、边数、边长,具体用到哪些则取决于我们的算法。
再次提醒:圆周率 = 边长 × 边数 ÷ (半径 × 2)。
圆内多边形的边数可以让用户输入,假设边数是n。
知道了边数,就知道了n边形相邻两边的夹角,等于内切角,即360÷n;也知道了多边形中单独一个三角形的内切角,等于360÷n。
据此分析,引出了两种编程算法:
- 方法一
从用户处获取n,并将圆的半径设置为固定值R,则,算出 多边形边长 = (sin(360÷n÷2))× R × 2,多边形周长 = 边长 × n,所以,圆周率 = 周长 ÷ (R × 2)。
这个算法的优点是:1)直径是精确值。不足之处是:1)画多边形困难 2)正弦函数对一些读者来说偏难。
- 方法二
从用户处获取n,并将多边形的边长设置为固定值L,程序每画出一条边后转360÷n度并继续画下一边,直到绘制完n条边,则,算出 多边形周长 = L × n,此法无法直接得到直径(可以通过画多边形过程“起点与n÷2处的点之间的长度”算出直径的约数d),所以,圆周率 = L × n ÷ d。
这个算法的优点是:1)周长是精确值 2)画多边形容易。不足之处是:1)求直径不直观。
综上分析,我们采用第二种方法作为我们本次的算法。
01 软件分析
需求说明:
编写一个计算程序,程序开始时让用户输入圆内多边形的边数n,从固定起点A开始绘制直线,直线长度为L,旋转360÷n度并继续画下一条边,以此类推,直到绘制完n条边。另外,在绘制第n÷2边时,记录下此时与A的距离,作为直径d。多边形绘制完成后,计算圆周率 = L × n ÷ d,在屏幕上显示结果。
需求分析:
- 至少需要两个角色,一个角色询问边数,一个角色绘图;
- 角色A通过输入框询问用户切割成几边形,存入变量n,并通知角色B画图和计算;
- 角色B画图:绘图起点设置在y轴上,暂定坐标x=0、y=160。试运行时如发现不妥,可以再调整;
- 多边形边长不能固定,而应该根据n的大小进行调整(请思考原因,此处不讲解了),暂定边长L=1000÷n;
- 循环n÷2次画多边形的一半:画直线L,然后旋转360÷n度并继续画下一边。循环结束时,记录下与起点的距离,即直径d;
- 继续循环n÷2次画多边形的另一半;
- 计算圆周率 = L × n ÷ d,计算结束,结果输出在屏幕上显示。
02 添加角色
默认的小猫角色用来询问用户,再增加一个角色用来画圆。
对于第二个角色,我们使用绘制的方式,画个圆点即可。操作步骤是,点击【选择一个角色】,选择【绘制】,在造型编辑器中(也就是Scratch自带的画图软件),点击【画笔】,因为我们要在造型的中心画一个小点,所以先放大造型背景图,在能看清中心十字星的时候,将鼠标移到中心之上,鼠标左键点击绘制一个小点。

03 调整角色的大小和位置
将角色调整到合适的大小,将小猫移到舞台的一角。
04 更换舞台背景
按照你自己的喜好,将默认的舞台背景替换成合适的背景图。
为了让大家看清楚,编程中我们使用的坐标,和绘制的圆的精确位置,我使用下面的图。如果你觉得不是很美观,可以在程序调试成功后替换成其他背景图。
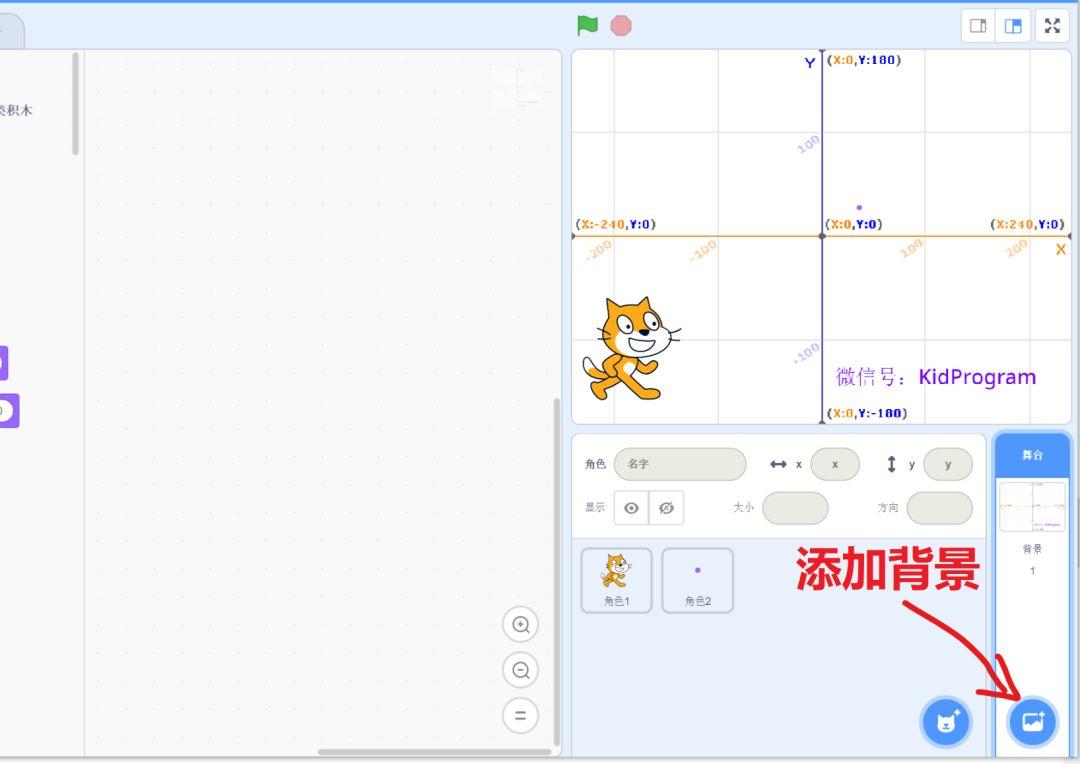
背景图的名字是Xy-grid。
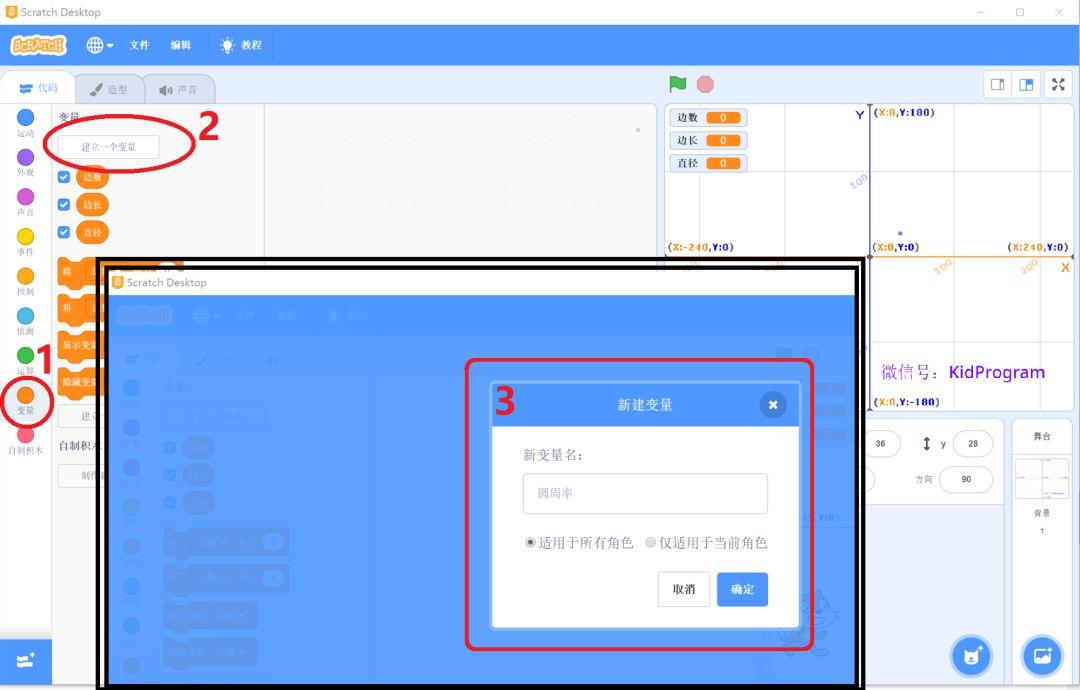
05 添加变量
增加4个变量:圆周率、边数、边长、直径。
06 小猫角色编码
小猫角色的编码很简单,询问多边形的边数,将变量值初始化归零。
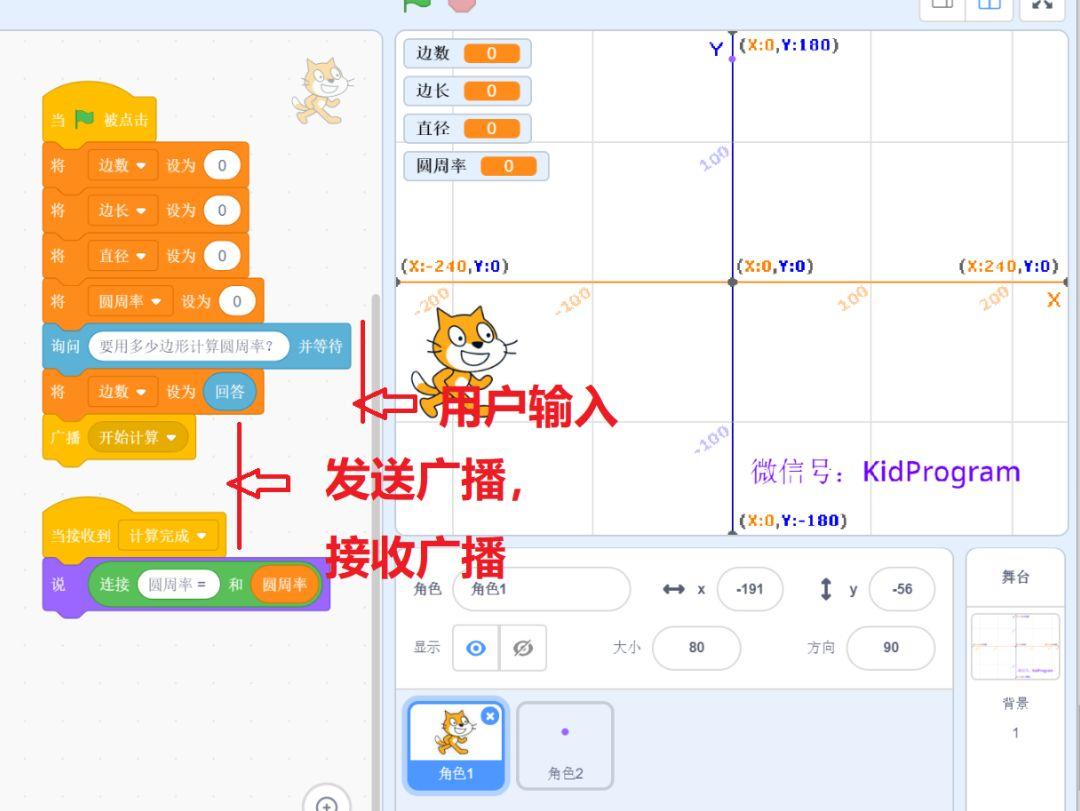
07 画图角色的编码
画图角色的编码和需求分析中是一致的,每个积木编码的含义详见下图的图注
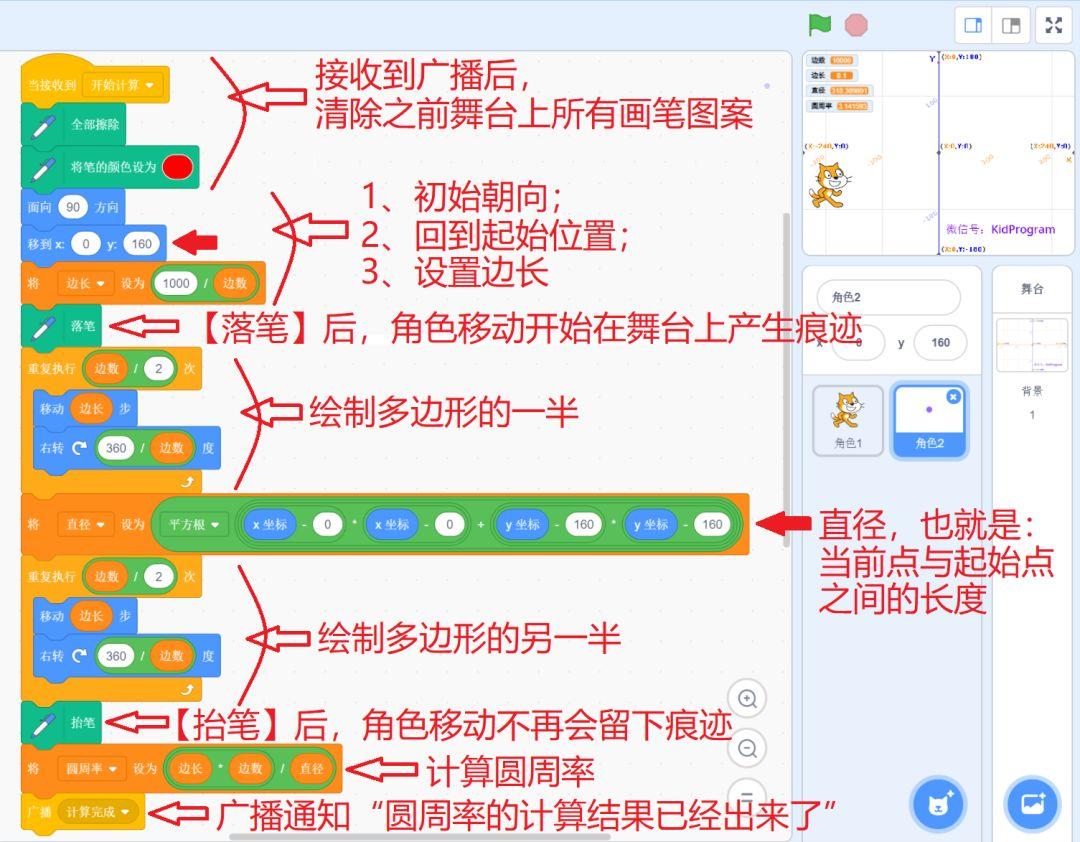
其中有些需要着重讲解:
1、角色的朝向与转交
多边形顶点时,角色的朝向与转角是比较难理解的内容。
请务必先自己思考,有了一定思路后,观察下图。
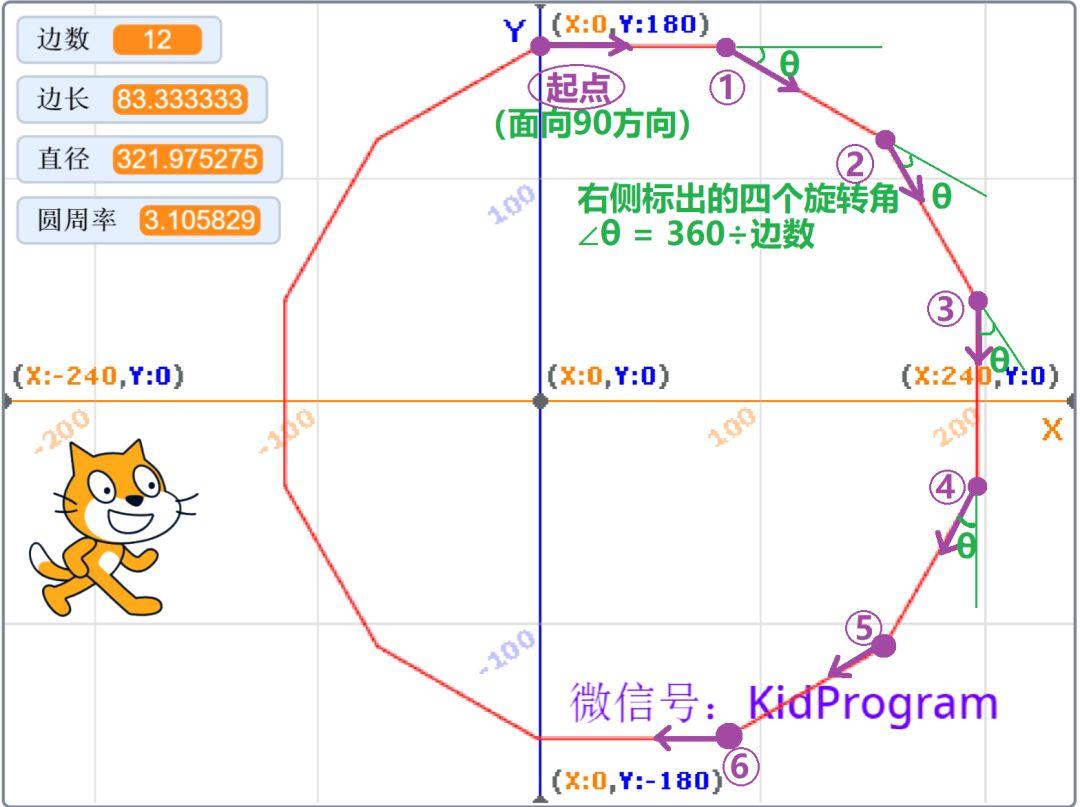
紫色箭头,表示了角色当前的朝向;
绿色θ角,表示了画下一条边之前,角色的旋转角;
2、“直径”计算
计算直径,其实就是计算“坐标系中两点的距离”。
计算两点距离有现成的方法,如下图
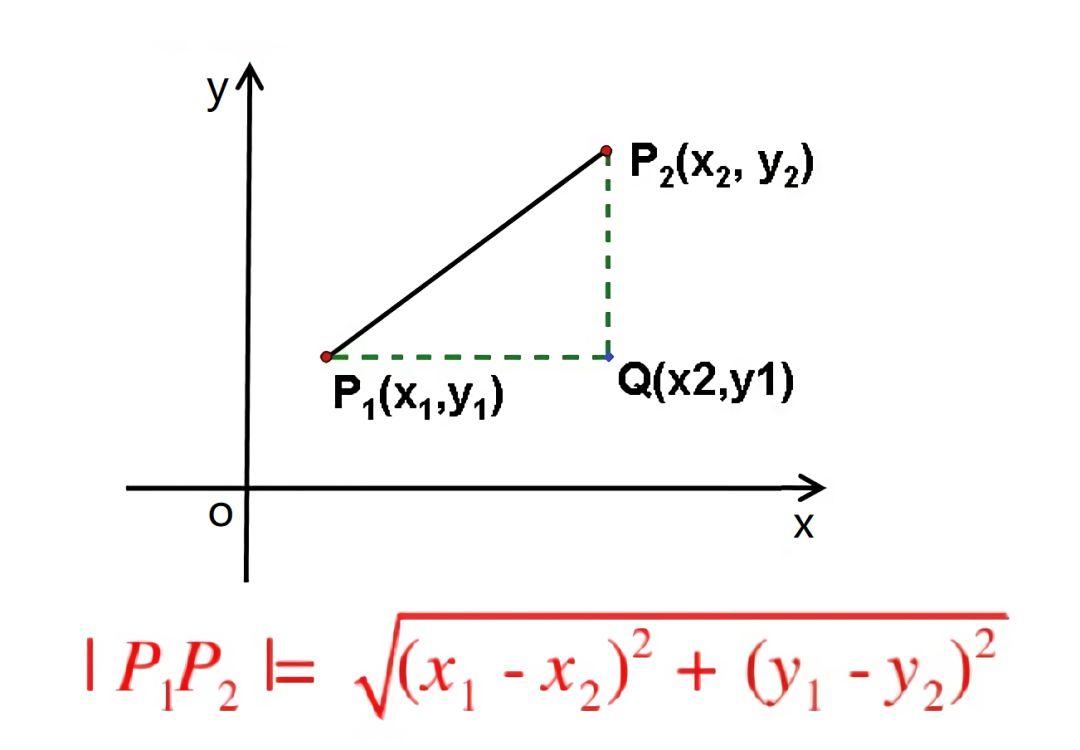
通过代码实现这个公式

上面的代码运行起来完全正确。可是,我总觉得有些不完美的地方:1)积木代码太长了,看起来麻烦 2)求两点距离的公式有的读者还没学习或难以理解运用。
针对“直径”计算,我们可以优化一下代码!
08 画图角色的编码(第2版)
一、添加一个新角色【起点】
首先,再增加一个角色【起点】,它一直固定在绘图的起点位置,除此之外,不做其他事情。
操作步骤:
1、给画图角色改一个“见名知意”的名字;
2、从画图角色复制一个新角色,并改名为“起点”;
3、删除因复制自带过来的代码;

4、编写新代码
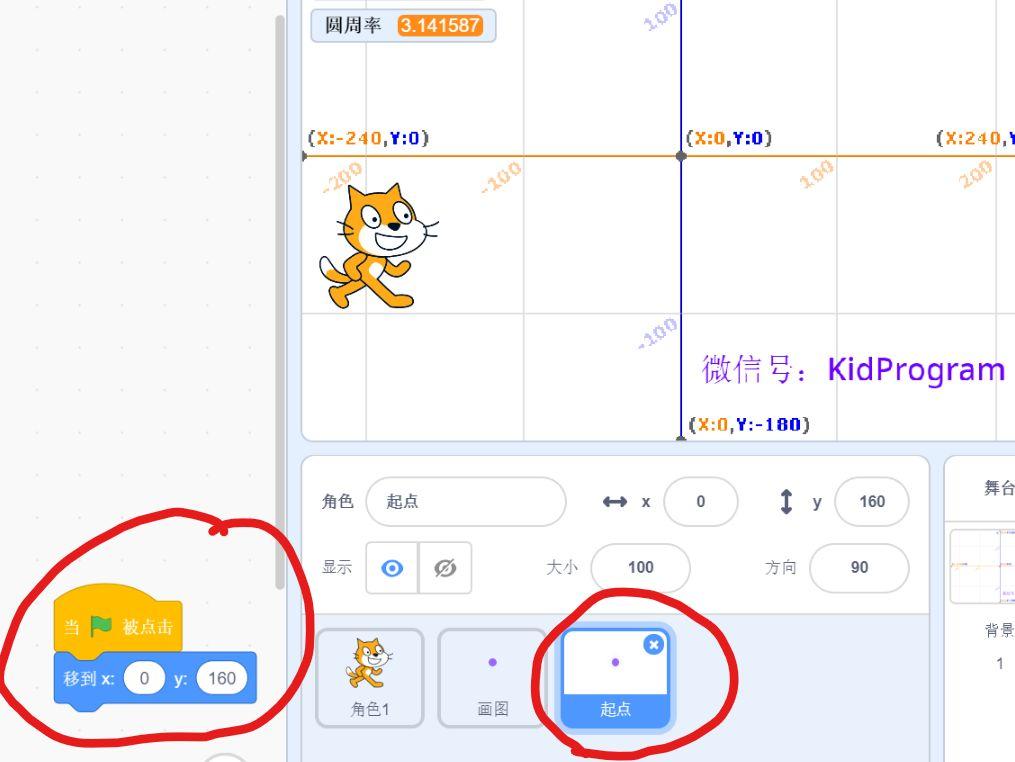
二、修改求直径的代码
然后,修改求直径的代码,只要求解【画图】角色与【起点】角色之间的距离即可。
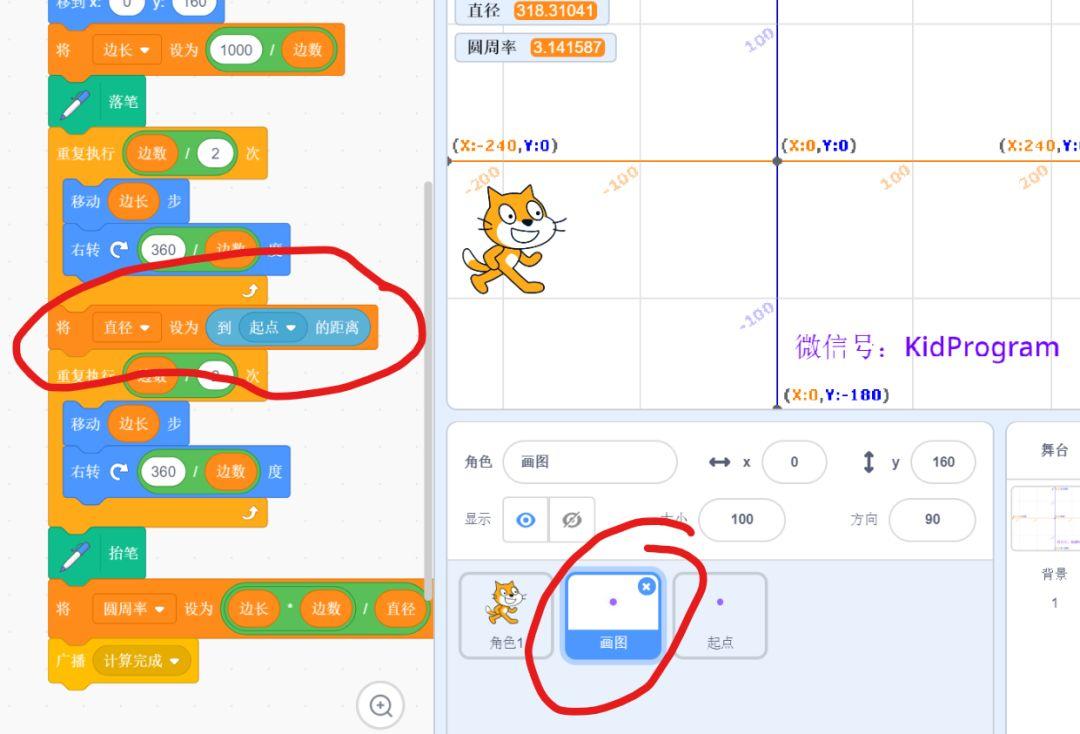
09 完工!运行程序
至此,我们完成了“需求说明”中的全部内容,可以点击舞台左上角的小旗子运行程序,查看效果。
但是,当你填写的边数特别大时,会发现程序运行了很长时间。如果你只想知道 π 的值而不关心动画过程,可以【打开加速模式】,这样程序就会瞬间运行完毕了。

附加练习
-
用户输入时,如果小于3,不进行计算,直接提醒用户输入值不合理(思考为什么要控制不能小于3)
-
去掉用户输入,将程序改成多边形边数从3开始逐渐增加,观察个变量和圆周率的变化

