友情提示：680元/半年，儿童学编程，就上码丁实验室。
求整数的最大公约数是小学数学里的一个知识点，方法有多种，数值比较小的可采用质因数分解法与短除法，比较好理解，也比较好用，但如果要计算的两个数数值较大时就有点困难了，这时候就用到更相减损法与辗转相除法。
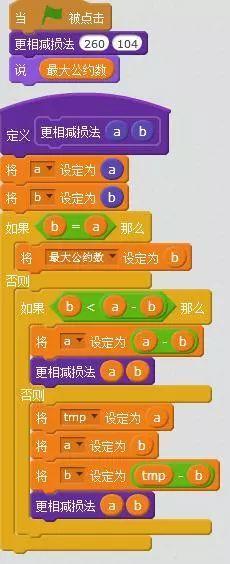
更相减损法：是出自我国《九章算术》的一种求最大公约数的算法，其步骤是：
所以，260与104的最大公约数等于13乘以第一步中约掉的两个2，即13*2*2=52。
更相减损法：图片代码传输错误
辗转相除法：也叫欧几里德算法，其计算原理是两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数。
最大公约数（Greatest Common Divisor）缩写为GCD。gcd(a,b) = gcd(b,a % b) (a % b ！= 0)
∴ （319，377）=29
辗转相除法：
计算上辗转相除法以除法为主，更相减损术以减法为主，计算次数上辗转相除法计算次数相对较少，特别当两个数字大小区别较大时计算次数的区别较明显。
手动求解最大公约数如果数值较小用短除法比较快，数值较大用欧几里得算法比较快。