niop-基础题库 “判断分数”

题目描述:

某次考试共有n道判断题，每道题m分；A打了a个钩，其余打叉，结果得了x分；B打了b个钩，其余打叉，结果得了y分；C一道都不会，索性全部打叉，那么至少蒙对了多少分？

输入格式:

共两行：

第一行输入两个正整数n、m，以空格隔开；

第二行输入四个正整数a、x、b、y，以空格隔开。

输出格式:

一个正整数，表示C至少蒙对的分数。

如果C可能一题也蒙不对，输出“2333”。

样例输入:

10 10
5 60 2 90

样例输出:

70

解题：

假设A同学打勾的a道题里，有p道题是答对的，可得出a-p道题是答错的；

打叉的题目中，有x/m-p道题是答对的，可得出n-x/m-a+p道题是答错的。

p既要小于等于a，也要小于等于x/m，所以p<=min(a, x/m)

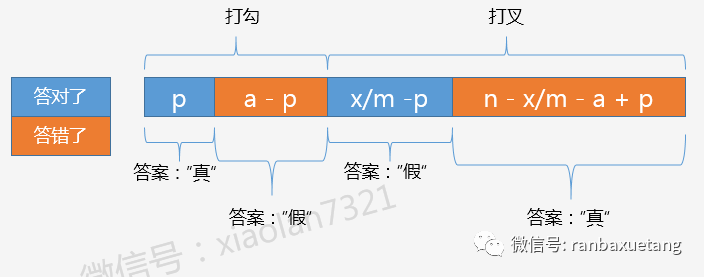
设，有cnt道题目的答案为“假”，则：

cnt = (a-p) + (x/m-p) = a+x/m-2*p, cnt是关于p的减函数。

if a<=x/m, cnt>=a+x/m-2*a=x/m-a

else, cnt>=a+x/m-2*x/m=a-x/m,

所以，cnt的最小值是abs(a-x/m)。

同理，B同学的情况下，cnt的最小值是abs(b-y/m)。

C同学押答案为“假”的题目，答案为“假”的题目数量应该是abs(a-x/m) 和 abs(b-y/m) 的最大值。

如果a=x/m，且b=y/m，有可能所有题目的答案都是“假”，从而造成C同学一题都蒙不对，因此输出“2333”。

代码：

#include<bits/stdc++.h>
using namespace std;int main()
{ 
  int n,m,a,x,b,y;
  cin >>n>>m;
  cin >>a>>x>>b>>y;
  if(a==x/m && b==y/m) cout << 2333;
  else cout << ((abs(a-x/m)>abs(b-y/m)) ? abs(a-x/m)*m : abs(b-y/m)*m);
  return 0;
}