码丁实验室,一站式儿童编程学习产品,寻地方代理合作共赢,微信联系:leon121393608。
翻译:现有一水池一丈见方,池中生有一棵初生的芦苇,露出水面一尺,如把它引向岸边,正好与岸边齐平,问水有多深,该芦苇有多长?(一丈等于十尺)

这一问题在世界数学史上很有影响。印度古代数学家婆什迦罗的《丽罗瓦提》一书中有按这一问题改编的”风动红莲”;阿拉伯数学家阿尔•卡西的《算术之钥》也有类似的”池中长茅”问题;欧洲《十六世纪的算术》一书中又有”圆池芦苇”问题。它们比我国要晚几百上千年。
我们的老祖宗真是太有文采了,能用文言文准确描述数学概念。
这就是大家都知道的勾股定理,我们不妨用现代的解法把它解出来。
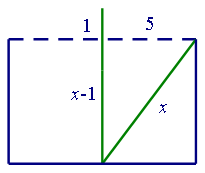
如图,设葭长为x丈,根据勾股定理有(x-1)²+5²=x²,解得x=13,故水深13-1=12丈,葭长13丈。
今天,我们不妨用Scratch来解一下这个古老的数学题,写出100以内所有的勾股数。
勾股数就是可以构成一个直角三角形三边的一组正整数。勾股定理:直角三角形两条直角边a、b的平方和等于斜边c的平方(a²+b²=c²)。

最小的勾股数是3、4、5。要避免3、4、5和4、3、5这样重复的勾股数,就要使三个数符合a<b<c的关系。该程序采用枚举算法,从3开始依次列举a、b、c三个变量的可能值,并使用勾股定理判断这三个变量值是否符合要求。如果符合勾股定理的要求,就把这三个变量记录到“勾股数”链表中。

编程过程如下:
先建立3个变量:
再建立一个列表,用于存放勾股数:
具体脚本如下:
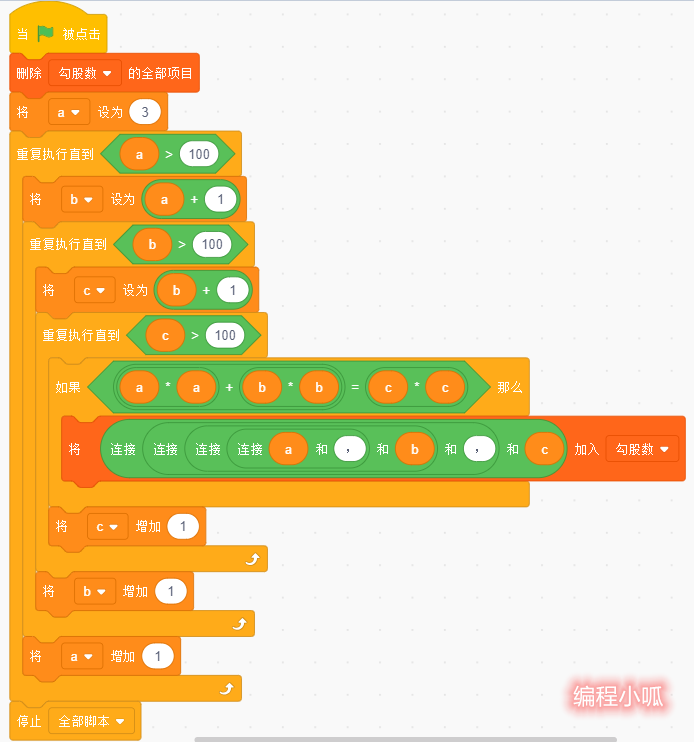
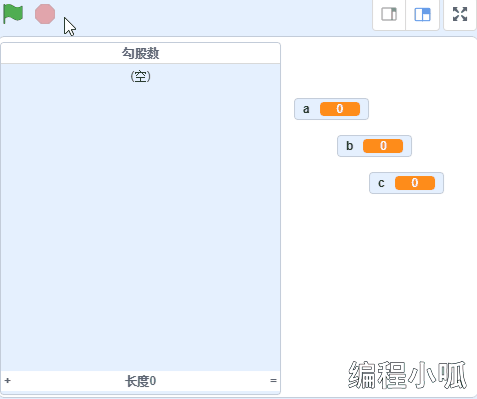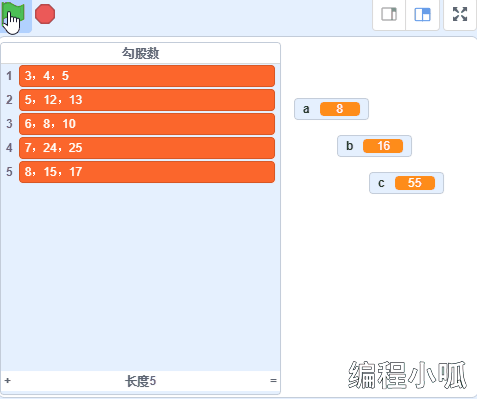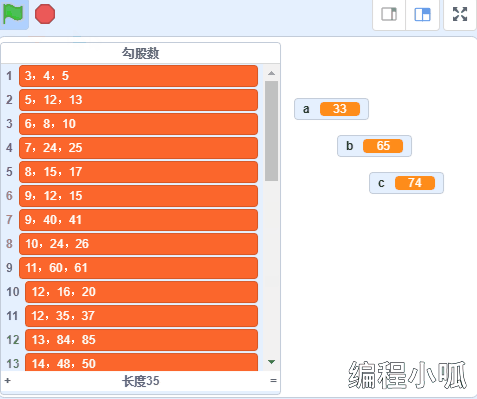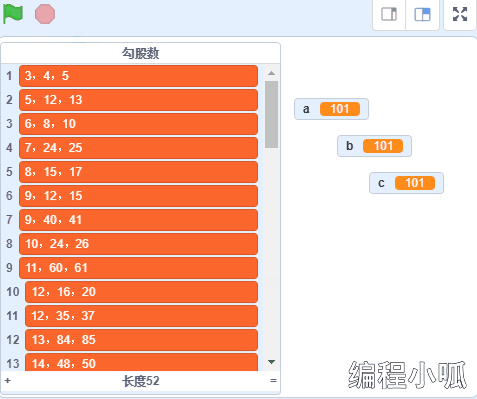
运行代码,将会得到100以内所有的勾股数,并记录到“勾股数”链表中。


原创不易,望大家且转且珍惜,需要转载请联系作者。
转自公众号:
编程小呱

