友情提示：380元/半年，儿童学编程，就上码丁实验室。
1
问题描述
任意一个边长是整数的长方形都可以分割成若干个边长是正整数的正方形，分割的方式有很多种，你需要找到分割出的所有正方形边长之和最小的那一种分割方法。
即将边长为正整数a，b的长方形划分成若干边长均为正整数，且每个正方形的边均平行于长方形的相应边，试求这些正方形边之和的最小值MlN。
如果这个长方形可以分成N个正方形，其中每个边长为ci，那么MIN=c1+c2+…+cN。注意，数组c中的元素可能相等。
输入
一共10行，每行两个正整数表示每个长方形的长和宽ai，bi。
输出
一共10行，每行一个整数，输出每个长方形分割出的正方形边长之和的最小值MIN。
样例输入
1 1
2 1
3 1
4 1
5 1
6 1
7 1
8 1
9 1
10 1
样例输出
1
2
3
4
5
6
7
8
9
10
数据范围
30% ai，bi≤MAXINT
100% ai，bi≤MAXLONGINT
2
问题分析
要求正方形的边长之和最小，那么切割下来的正方形应当尽可能大。
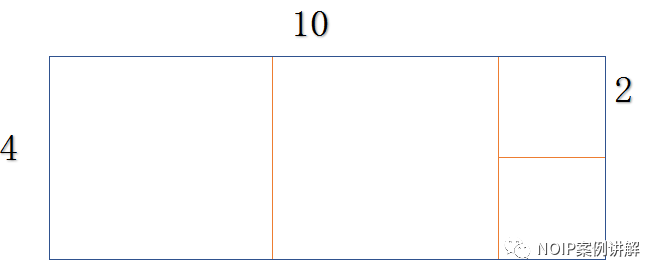
按照上图的切法，得到两个4*4和两个2*2的正方形，边长之和为12。这种方法得到的正方形的边长之和最小。
3
参考代码如下
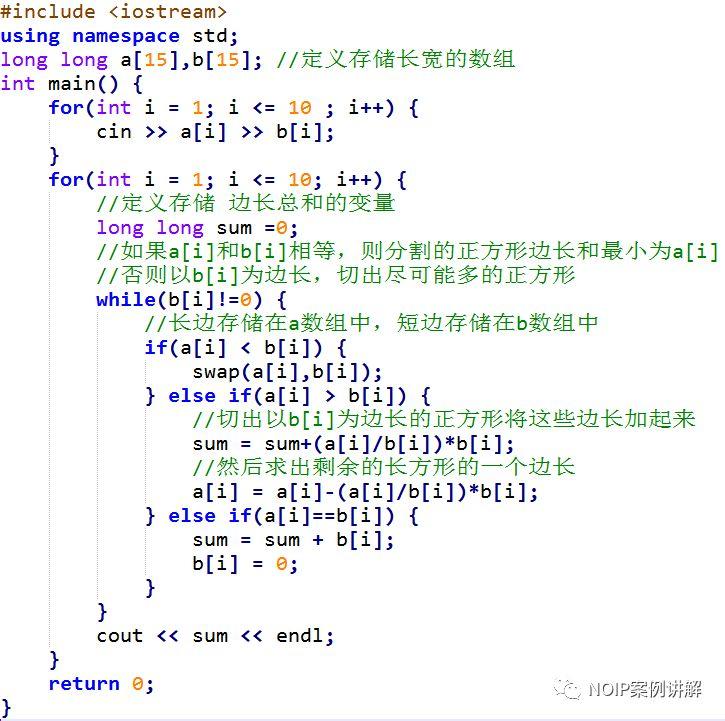
转自公众号：
信息学少儿编程