友情提示：视频教程观看时请手动设置清晰度。
第四讲 Scratch编程思想与数学问题（二）
本讲通过Scratch编程与数学问题的结合，讲解计算机编程中的思想，并利用Scratch求解三个典型的数学问题。
第四讲的第二节，主要讲解递归的思想，并通过递归法，求解数学中的求最大公约数问题。程序运行效果请看视频。
一、欧几里得法求两个数的最大公约数简介
最大公约数，也叫最大公因数，是指两个或多个整数的公因数中最大的一个。计算最大公因数的方法有很多种，其中最为迅速的一种算法，被称之为欧几里得算法，也叫做辗转相除法。
设a和b为两个正整数（假设a>b），用欧几里得算法求两个数的最大公约数的步骤如下：
用a除以b，得a/b=q1……r1（表示商q1，余r1），如果r1=0，则a，b的最大公约数为b。
如果r1≠0，则a，b的最大公约数等于b和r1的最大公约数。
再用b除以r1，得b/r1=q2……r2（商q2，余r2），如果r2=0，则b与r1的最大公约数为r1。否则，b与r1的最大公约数等于r1与r2的最大公约数（r1与r2的最大公约数等于a与b的最大公约数）。
以此类推，不断的辗转相除除数与余数，直到能整除为止。
当余数为0时的那个最后一个除数，就等于a，b两个数的最大公约数。
欧几里得算法基于如下原理：两个整数的最大公约数等于其中较小的数和两数相除的余数的最大公约数。（这个定理的证明并不复杂，请小朋友仔细思考一下，也可以自己去寻找相关的书籍来学习哦）。
例如，123456 和 7890 的最大公因子是 6，这可由下列步骤看出：
|
被除数 |
除数 |
余数 |
|
123456 |
7890 |
5106 |
|
7890 |
5106 |
2784 |
|
5106 |
2784 |
2322 |
|
2784 |
2322 |
462 |
|
2322 |
462 |
12 |
|
462 |
12 |
6 |
|
12 |
6 |
0 |
二、用递归思想来实现欧几里得算法
我们在上面欧几里得算法的学习中发现，算法实际上是不断的在重复一组被除数÷除数得出余数的过程，这个过程持续多少次事先无法知道，完全取决于被除数与除数。
我们在前面的学习中已经知道，在Scrath中有一种自定义功能块的指令，这个指令可以把一组需要经常使用的指令打包成一条语句，以方便在编写程序中调用。这里我们就是使用这个指令，来实现一种递归的逻辑算法。
递归是一种逻辑算法，他表示一个功能块（在实际编程中被称为程序）调用它自己的过程，递归作为一种算法，在编程中被普遍使用，它能够把一个比较大的复杂问题，转化为一个与原始问题类似，但是规模更小的问题，通过层层的递归，最终实现解决问题的目的。
在欧几里得算法中，我们是在不断层层递归被除数除以除数得出余数的过程。
三、Scratch编程求最大公因数的代码
首先新建三个变量，分别命名为：被除数、除数、余数
在更多模块指令集中，新建功能块，如下
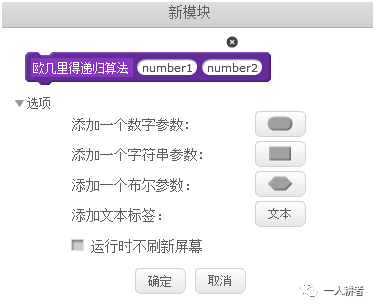
其中number1，number2，点击选项下面的添加一个数字参数可以得到。
定义好的功能块是一个带参数的功能块，在脚本区会出现这样一个功能块的起始标签。
这里的number1和number2是编写功能块代码时内部使用的参数。这条语句在指令区的显示如图
继续编写如下代码
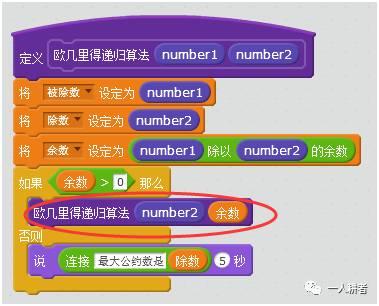
这里，首先将三个变量分别赋值为number1，number2和两数相除的余数。下面通过一条判断语句对余数的结果进行判断。如果余数>0说明这个时候没有被整除，那么需要继续通过欧几里得算法进行计算，因此这个功能块调用了自身，只不过调用的时候，相应的参数进行了修改，把number2作为被除数，把余数作为除数。
如果余数>0不成立，说明这个时候余数为0能够整除，那么根据算法，这个时候的除数就是最大公约数，因此下面的语句输出目前的除数。
最后，编写如下代码，提示用户输入两个数字，程序就可以自动完成最大公约数的计算了。
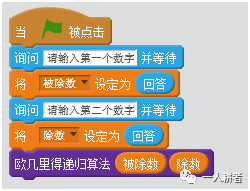
递归的思想是编程中常用的思想，但是对于初学者来说，这个逻辑可能会有些难以理解，请小朋友仔细思考这部分代码，对照第一部分的列表分步思考程序每一次调用自身时，被除数、除数、余数的变化情况，相信大家很快就可以掌握递归的使用技巧。
始发于微信公众号：
一人耕者