小学奥数与北京中考

 

小学阶段为什么要学习奥数？这个问题有很多解答，其中一个是：小学奥数与中考和高考的解答题有着千丝万缕的联系。

 

例题：已知一个二次函数的图象经过A（3，0）、B（0，-3）、C（-2，5）三点。

（1）求这个函数的解析式；

（2）画出这个二次函数的图象（草图），设它的顶点为P，求△ABP的面积。

 

解答：1）设二次函数解析式为y=ax²+bx+c，

将A、B及C坐标代入得：

则函数解析式为y=x²-2x-3；

 

（2）y=x²-2x-3=(x-1)²-4，因此对称轴为x=1，P点坐标（1,4）。

画出草图，如图所示。

 

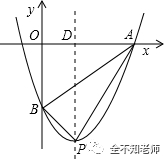
其中OB=3，DP=4，OD=1，OA=3，AD=OA-OD=2。则有，

 

 

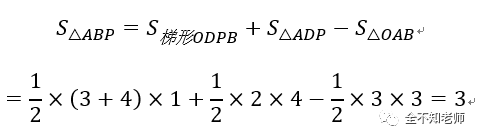
解析：二次函数是初中数学重要的考点之一。本题第一问求二次函数的解析式，直接利用待定系数法，解三元一次方程即可。第二问，需要先配方，进而利用二次函数的性质，求得对称轴以及顶点P的坐标，并画出图像(草图)。真正有难度的是求△ABP的面积。

 

中考的题目一般综合性较强。例如本题，即考察了二次函数的一般形式，又考察了配方后的形式。即有一元二次方程的求解，又有多元一次方程组的求解。最后还考察描点连线，以及通过数形结合，求特殊三角形的面积。

 

三角形ABP的面积，给出的解答是利用割补法，将面积不容易求解的三角形转化为面积容易求解的三角形和梯形等的组合。本题如果利用海伦公式求解，会落入出题者的陷阱。因为根据各点坐标，可以得出各边的长度。但是三边的边长分别为

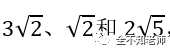
利用海伦公式求解，计算相当繁琐。

 

而三角形ABP面积最简洁的求法是利用等积变形。具体如下图所示：

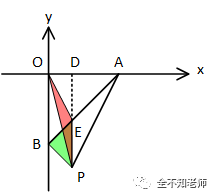
设二次函数的对称轴为DP，与x轴的交点为D。AB与DP的交点为E。因为DP平行于OB，因此可以将三角形BEP的边PE保持不变，将点B平移到点O。即三角形BEP的面积等于三角形OEP的面积。

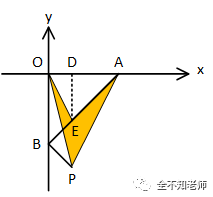
因此三角形ABP的面积等于三角形OEP与三角形AEP的面积之和。而这个图形的面积等于三角形POA的面积减去三角形EOA的面积。

 

三角形POA与三角形EOA是同底的，底边都是OA，长度为3。三角形POA在OA上的高为DP，长度为4；三角形EOA在OA上的高为DE。由于OA=OB=3，所以三角形OAB为等腰直角三角形，∠OAB=45°。因此三角形DAE也是等腰直角三角形，DE=DA=3-1=2。从而有：

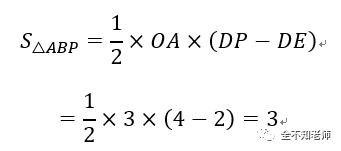
小奥知识点：割补法求面积以及等积变形。其中等积变形是小学奥数极具特色的知识点，限于篇幅，这里不做展开。

 

总结：小学奥数的知识点与中考和高考有着千丝万缕的联系。本文通过一个中考的二次函数综合题进行了说明。请关注本公众号，后续会陆续给出其他的案例。