题目：七位数8□□□□□□3的各位数字互不相同，且是99的倍数，那么这个七位数最小是多少？
分析：最值问题常用的思路是：先“最”再“对”。意思是先找到最值，然后再进行调整，使之符合条件。对于本题而言，各位数字互不相同，而且要最小，显然应该是8012□□3的形式。
百位和十位数字应根据是99的倍数这一条件进行选择。99=9×11。所以各位数字之和是9的倍数，而且奇数位数字之和与偶数位数字之和的差是11的倍数。
解答：设七位数为8abcde3。
若要该七位数最小，则a=0，b=1，c=2。七位数为8012de3。
因为它是99的倍数，而99=9×11。因此，有
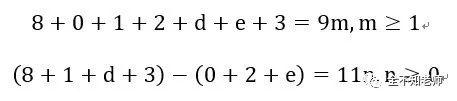
其中m、n为正整数。
化简后，为
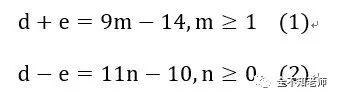
对于(1)式的不定方程，让m分别取值1，2，3，……，有
|
m |
9m-14 |
是否可取 |
|
1 |
-5 |
× |
|
2 |
4 |
× |
|
3 |
13 |
√ |
|
4 |
22 |
× |
当m=1时，d+e为负值，不可能；当m=2时，d+e为4，而1和3已经用了，所以也不可能；当m取4及以上值时，d+e为22及以上，这也不可能，因为两个一位数相加最大是8+9=17。
m只能取3，即d+e=13。从而d、e只能取6、7或7、6。
对于(2)式的不定方程，让n分别取值0、1、2、……，有
|
n |
11n-10 |
是否可取 |
|
0 |
-10 |
× |
|
1 |
1 |
√ |
|
2 |
12 |
√ |
当n=0时，d-e为-10，不可能；当n取2及以上值时，d-e为12及以上，这也不可能。因为两个一位数相减最大是9-0=9。
n只能取1，即d-e=1。从而d=7，e=6。
所求的七位数为：8012763。
后记：本题是最值问题与数论结合的综合性题目。最值问题要运用“先最再对”的策略，数论部分要熟悉9和11整倍数的特点。题目设计的很巧妙，相当有难度。
始发于微信公众号：
全不知老师