2018年高考数学(理科)全国卷1第10题的数学背景

题目：下图来自古希腊数学家西波尔克拉底所研究的结合图形。此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC，直角边AB，AC。△ABC的三边所围成的区域记为I，黑色部分记为II，其余部分记为III。在整个图形中随机取一点，此点取自I，II，III的概率分别为p₁，p₂，p₃，则（）

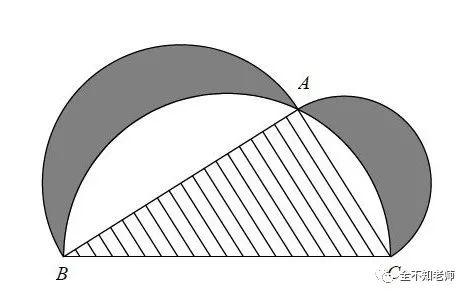
A.p₁=p₂  B.p₁=p₃  C.p₂=p₃  D.p₁=p₂+p₃

 

 

数学背景：在英国著名数学史家J. F. 斯科特所著的《数学史》一书第23-24页中写到：

“但是希波克拉底最容易使人记得的一件事，就是他证明了半月形面积可以化为三角形的面积，这是把曲线形面积化为直线形面积的第一个例子。他还熟悉这样一个事实：圆面积与其直径的平方成正比。由此他从一个等腰直角三角形ABC（图2）出发，在三条边上各做一个半圆。根据毕达哥拉斯定理，AB上那个半圆的面积等于AC和CB上两个半圆的面积之和。如果现在从整个图中移去AB上的半圆，则留下的两个相等的半月形。但如果从同一图中移去两个相等边上的半圆，则只剩下三角形ABC。所以三角形ABC的面积一定等于两个半月形的面积。正是由于希波克拉底证明了曲线的面积能化为直线形的面积，才激起了他对求积问题的兴趣。”

 

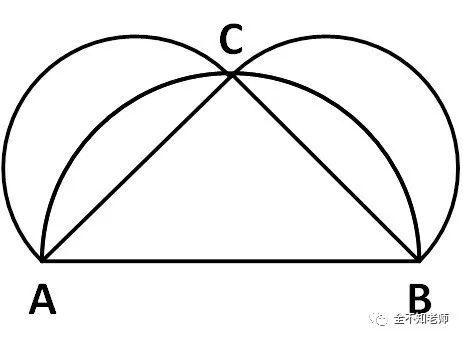
图2

 

该书是不可多得的汉译经典。由侯德润、张兰翻译，译林出版社出版，2015年9月第2次印刷。

解释：书中的叙述比较枯燥。我们按照其叙述，对相关图形涂色，就一目了然了。

 

如图3所示，涂色的图形是AC和CB上两个半圆的面积之和。

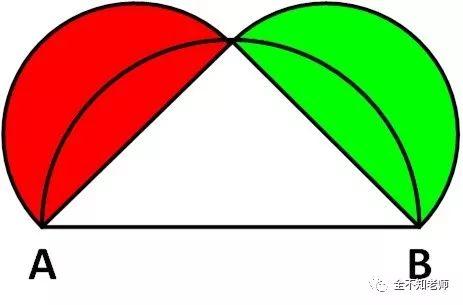
图3

 

如图4所示，涂色的图形是AB上那个半圆的面积。

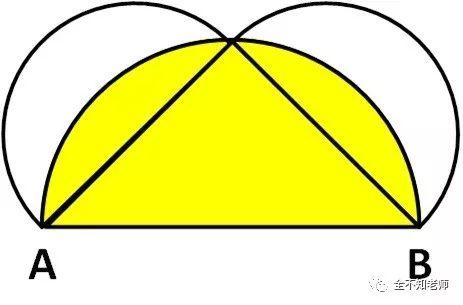
图4

根据勾股定理，这两部分面积相等。将公共部分去掉后，分别如图5和图6所示，它们的面积也相等。

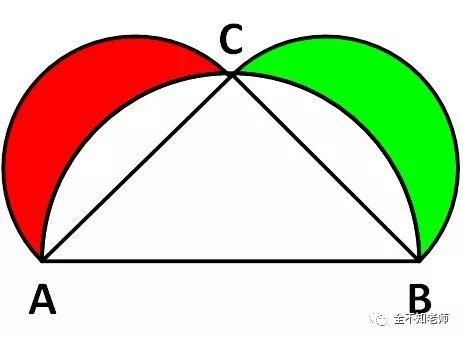
图5

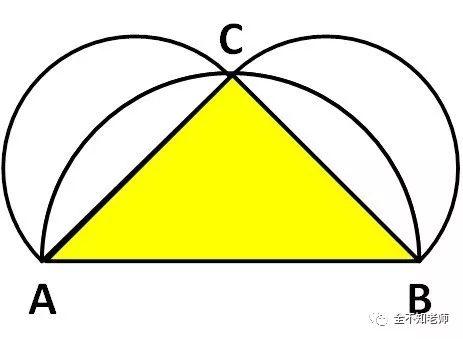
图6

后记：高考题中，还综合了概率的知识点。即几何概型，在总图形固定的前提下，事件的概率只与所在区域的面积成正比。显然只有区域I和区域II的面积相等，与区域III的面积不一定相等。而且区域I的面积也不等于区域II和区域III的面积和。

始发于微信公众号：
全不知老师