日本小学的入学试题

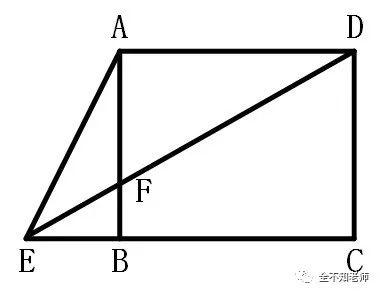
题目：在矩形ABCD中，BC的长度为10cm，CD的长度为8cm。点E为CB延长线上的一点，连接EA和ED，其中ED与AB相交于点F。已知△AFD和△BEF的面积差为24cm²，求△AED的面积和BE的长度。

 

背景：这是去年某位小同学去日本小学面试遇到的一个题目，可能是倒数第二题。难度相当于我国初中二年级的水平。

 

解法：根据题意：△AFD和△BEF的面积差为24cm²。

    在Rt△AFD中，∣AD∣=10cm，令∣AF∣=xcm。

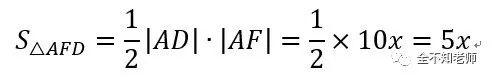
在Rt△BEF中，∣BF∣=(8-x)cm，令∣BE∣=ycm。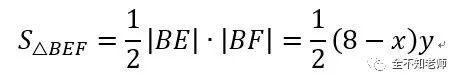

因此，有

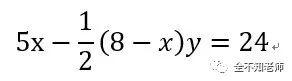
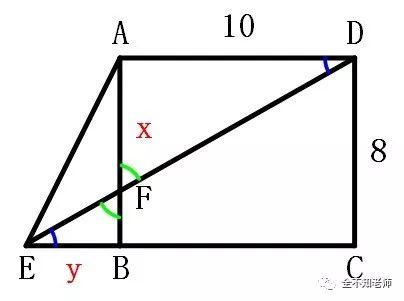
又，在矩形ABCD中，AD∥BC，因此 ∠ADF=∠BEF。

而∠AFD和∠BFE是对顶角，所以 ∠AFD=∠BFE。

于是△BFE∽△AFD。从而，有

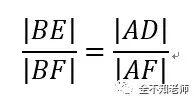
即

 

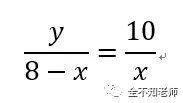
联立上述方程，得

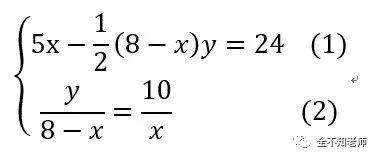
由(2)式得，

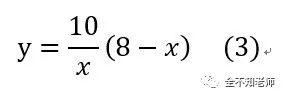
将(3)式代入(1)式，

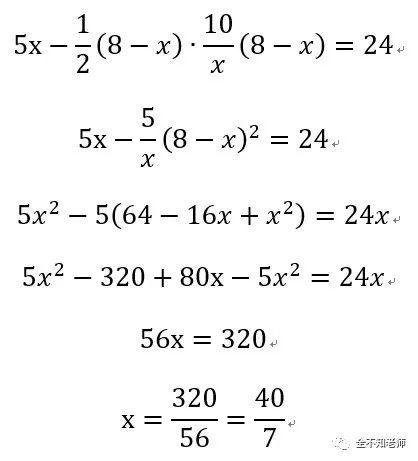
代入(3)式，得

 

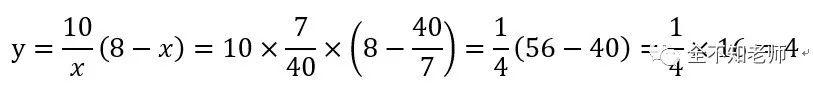
即有，

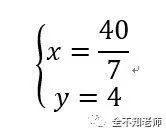
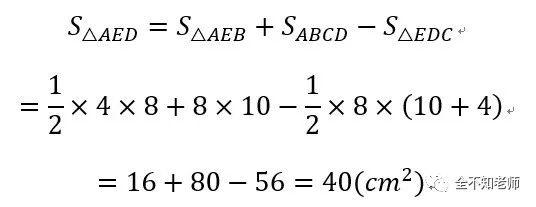
答：△AED的面积为40 cm²，BE的长度为4cm。

 

分析：本题是典型的“数”“形”结合题目。其中即有代数中的“三角形的面积计算”、“二元二次方程组”等与“数”相关的知识点，又有平面几何的“两条平行线之间的夹角相等”、“相似三角形对角相等和对边成比例”等与“形”相关的知识点。

 

其中解方程中不但涉及了二元方程组的消元，还隐含考察了一元二次方程的求解。虽然最后由于凑巧，二次项消掉，只需要解一元一次方程，但是在运算过程中有体现。

 

本题不需要太高难的技巧，但是考察的知识点较多，而且属于综合题目，难度中上。因此作为超前教育，考察学生的学习进度非常合适。

 

后记：本题涉及较多的化简和计算，尤其是有分数运算和平方和公式。对于普通中学生而言，都略有难度。如果是超前学习的小学生，难度会更大。

 

始发于微信公众号：
全不知老师