码丁实验室,一站式儿童编程学习产品,寻地方代理合作共赢,微信联系:leon121393608。
第六节 条件限定法——变量与过程
在开始编写程序之前,首先将此前已经完成的项目另存为“汉诺塔2”,并在汉诺塔2的基础上,编写新的程序。原有项目中需要保留的全局变量及过程如图30所示。
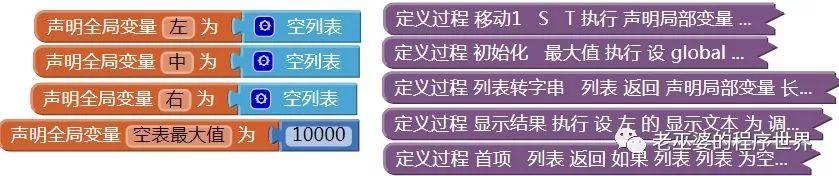
图30 需要保留的全局变量及过程
一、新增变量与过程完善
图30中部分过程需要加以完善,为此要先添加两个全局变量,如图31所示。

图31 添加两个全局变量
全局变量“最后移动项”用来保存上一次移动的数字,“步数”用来保存已经移动的步数。
需要完善的过程有两个——移动1过程及初始化过程,如图32所示,在这两个过程中对新添加的全局变量进行设置,并在初始化过程中增加对显示结果过程的调用。
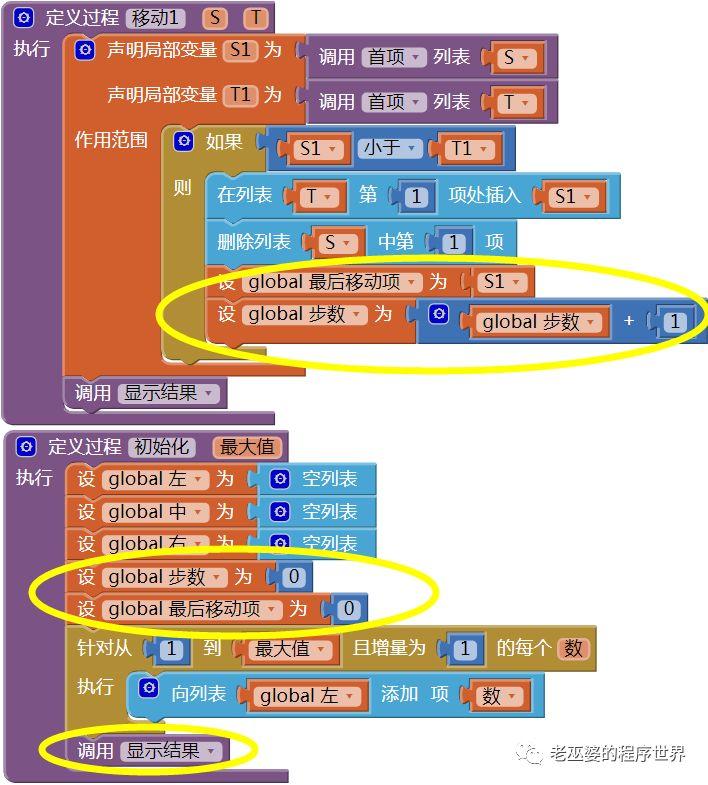
图32 完善过程,对新添加的全局变量进行设置
针对每一次移动,记录被移动的数字——最后移动项,以及移动的步数。在即将编写的程序中,最后移动项用来确定下一次移动的出发点。
二、创建新过程
(1)有返回值的过程——是偶数
根据第五节的结论c,在移动数字1时,如果塔高为奇数,则移动到落脚点,否则,移动到相对缓冲区,因此定义一个有返回值的过程——是偶数,以便根据塔高决定数字“1”的落脚点,代码如图33所示。

图33 有返回值过程——是偶数
(2)有返回值的过程——任务完成
如图34所示,当左侧的数字全部移动到右侧时,该过程的返回值为真。
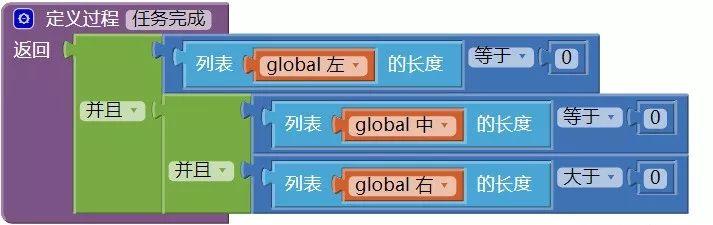
图34 有返回值的过程——任务完成
(3)有返回值的过程——塔高
根据第五节的结论d计算塔高。在计算塔高时,需要留心一种可能存在的情况。举例说明,假设实际塔高为5,那么它可能是(1,2,3,4,5),但也可能是(1,2,3,7,8),我们需要识别出这两种情况,前者的塔高=5,而后者的塔高=3。实际上我们要求的塔高必须是列表中最小的、且连续差值为1的数字的个数,因此,一旦遇到两个连续项的差不等于1,则塔高的值就已经确定了。塔高过程的代码如图35所示,一旦两个连续项的差值≠1,则设索引值为空表最大值,立即退出循环,返回计算结果。
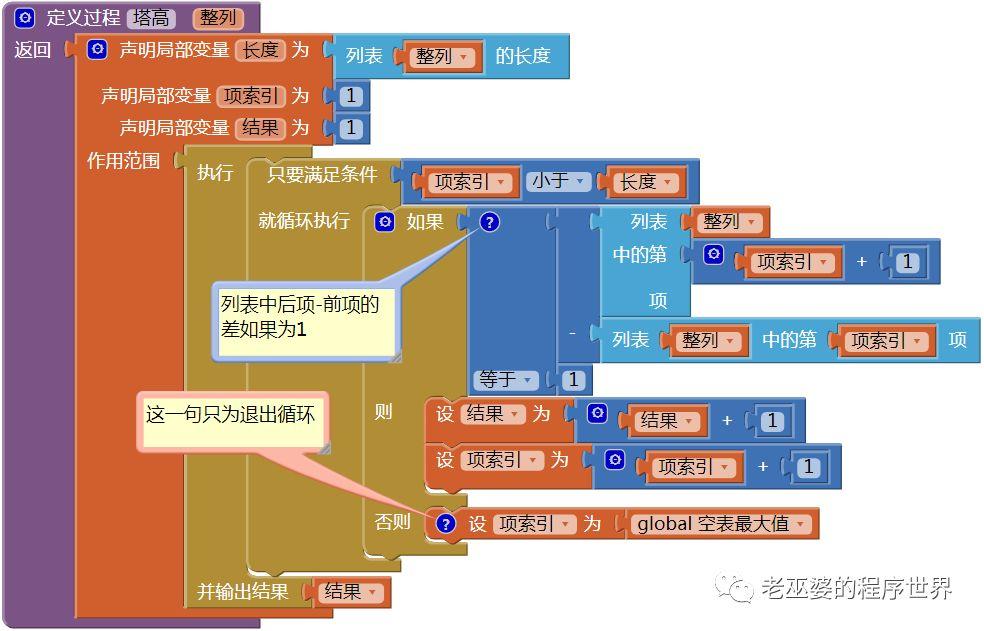
图35 有返回值过程——塔高
(4)有返回值的过程——出发点
根据第五节中给出的证明:每一次移动的出发点都是唯一的。如果不是第一次移动,则可以利用全局变量最后移动项,排除掉三分之一的选项(上一次移动的落脚点),然后在剩余的三分之二选项中,选择首项值较小者为出发点。(在上一节我们已经证明:如果选择首项值较大者为出发点,那么它将无法找到符合游戏规则的落脚点。)根据这一结论编写一个有返回值的过程——出发点,代码如图36所示。
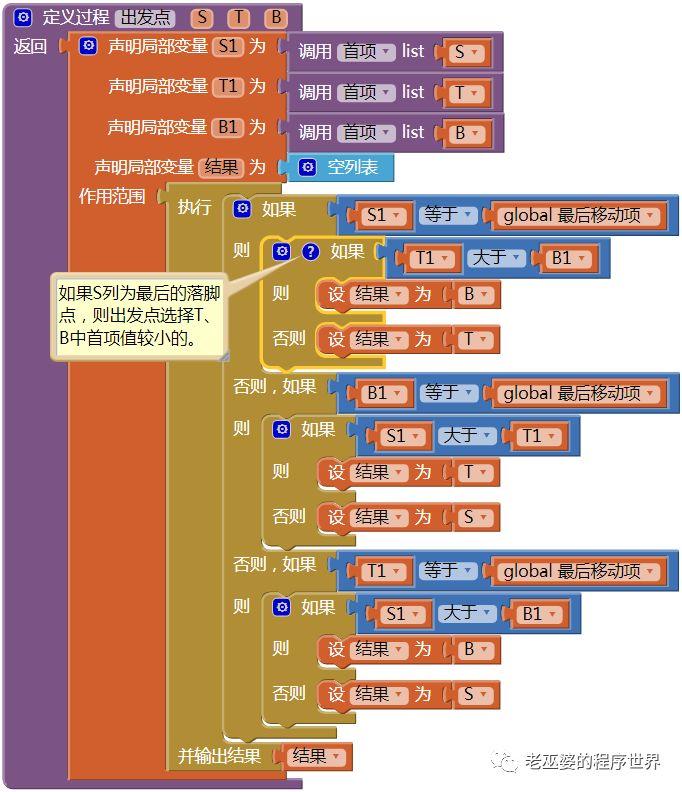
图36 有返回值的过程——出发点
(5)有返回值的过程——落脚点
根据第五节的结论b,当出发点的数字≠1时,落脚点是唯一的。我们来定义过程,求出这个唯一的落脚点,代码如图37所示。
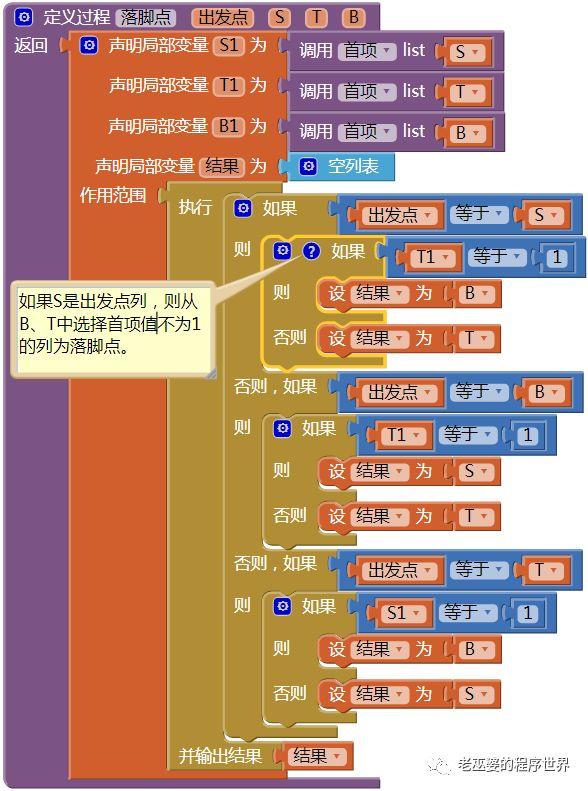
图37 有返回值的过程——落脚点
(6)有返回值的过程——塔尖落脚点
上面已经求出了被移动数字≠1时的落脚点,现在来解决被移动数字=1时的落脚点问题。根据第五节的结论c,“塔”的落脚点是唯一的,但塔尖的“1”落脚点不唯一,它与塔高有关,当塔高为奇数时,塔与塔尖(数字1)的落脚点相同,反之则不同。根据结论c,塔落脚点的首项值与出发点的塔底值相差1,据此确定塔尖的落脚点,相应的过程代码如图38所示。在判断S、T、B是否为出发点时,程序中使用了“S1=1”这样的条件,它等同于“S=出发点”这样的条件,但是前者是数值之间的比较,而后者是列表之间的比较,后者会消耗更多的计算力。
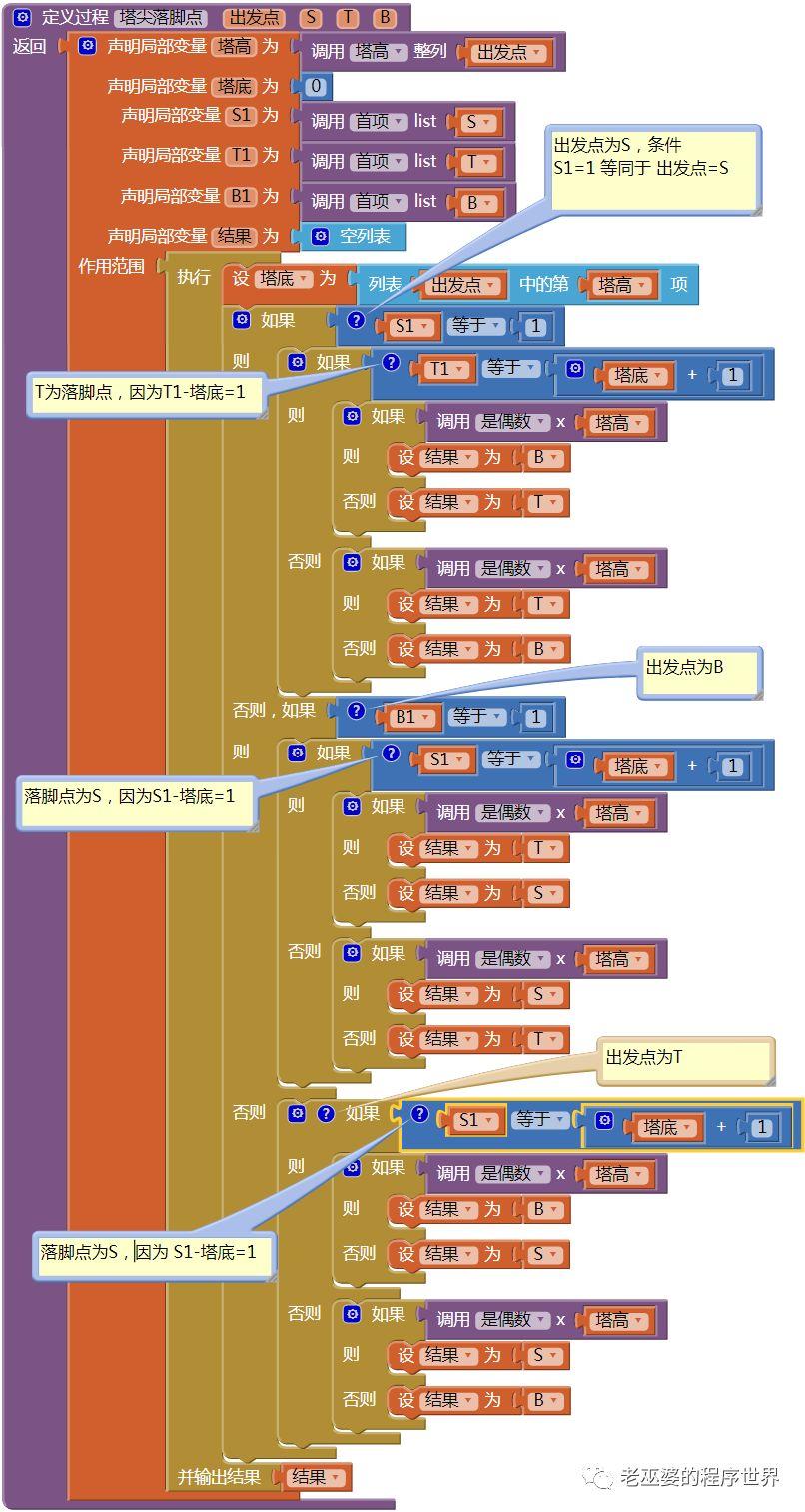
图38 有返回值的过程——塔尖落脚点
我们依据第五节中的4个条件及4个结论,确定了每一次移动的出发点及落脚点。如上所述,其实每一步移动都可以在前一步的基础上,确定唯一的移动路径,这样的结果得益于对物理世界中移动过程的观察、分析及归纳。运用人类自身的智能,可以极大地提高机器解决问题的效率,而这正是我们希望获得的能力。
有了上面的过程,我们就有了每次移动的出发点及落脚点,因此余下的事情就简单了。
== 未完待续 ==

