码丁实验室,一站式儿童编程学习产品,寻地方代理合作共赢,微信联系:leon121393608。
第八节 求解过程小结
我们已经完成了对数字(盘子)的移动,并成功地演示了数字的移动过程。阅读并理解前面几节中的程序并不难,就这个例子而言,难的不是程序,而是编写程序之前对移动规律的归纳与整理,这也正是我们希望通过学习编程培养所谓计算思维的最好途径。
在正式动手编写程序之前,我们三人小组经过了大约两周时间的摸索(各自还有另外的事情需要完成),时不时还会在一起讨论,相互提示,相互启发,如此才确定下来第五节中列出的若干个条件及结论。现将部分分析过程整理出来,虽然有的资料对解决这个问题没有帮助,但也不失为一种探索手段,或许可以为解决其他问题提供思路。
首先来看表2,表格中第一行数字为塔高,用N表示,每个数字下方是N个数字的移动路径,其中s代表起点,即左侧的列,b代表缓冲区,即中间的列,t代表终点,即右侧的列。从表格中可以发现一些规律,如,塔高为奇数时,第一步移动的落脚点均为t,而塔高为偶数时,第一步的落脚点均为b。此外,移动的步数均为奇数,居中的一步均为st,且紧邻st之后的一步也与塔高的奇偶具有相关性。这样的表格为分析数字移动的规律提供了直观的线索(为了缩短表格的长度,塔高为6的列被拆成两列6_1与6_2)。
表2 不同塔高时盘子的移动顺序
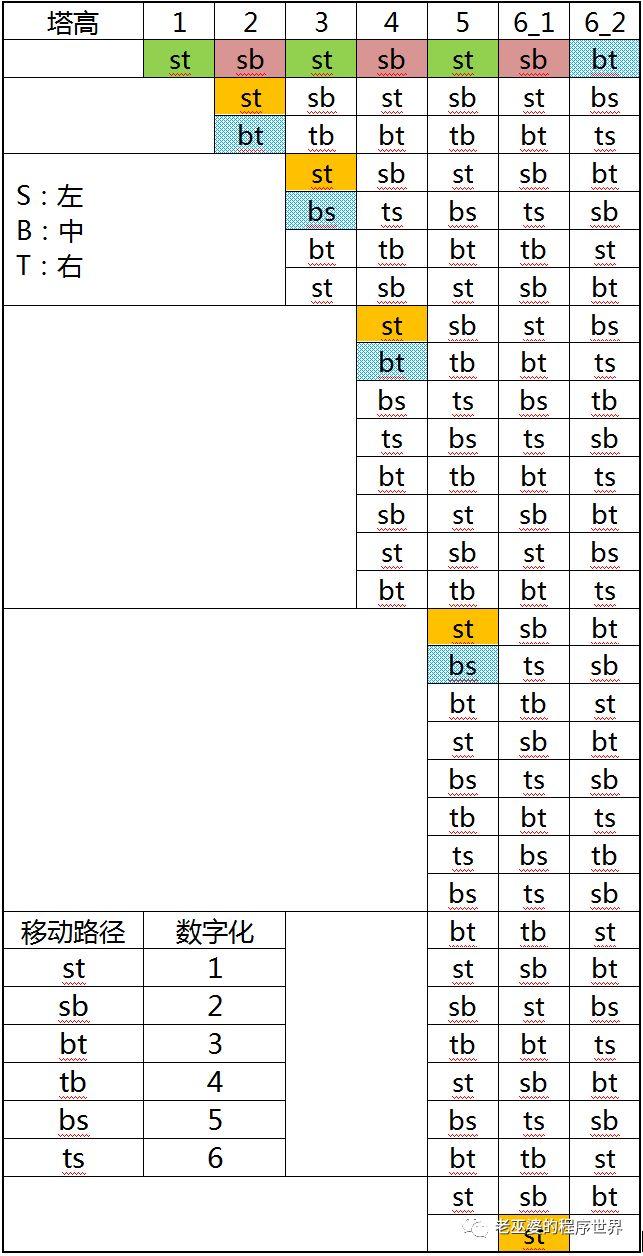
在表2中,左下角的移动路径与数字化两个子列,是为了绘制下面的图形而设定的。将六种可能的移动路径用数字来代替,我们可以在excel中利用表中的数据绘制相关的图形,如图43所示。这是针对塔高为6的数据绘制的图形。
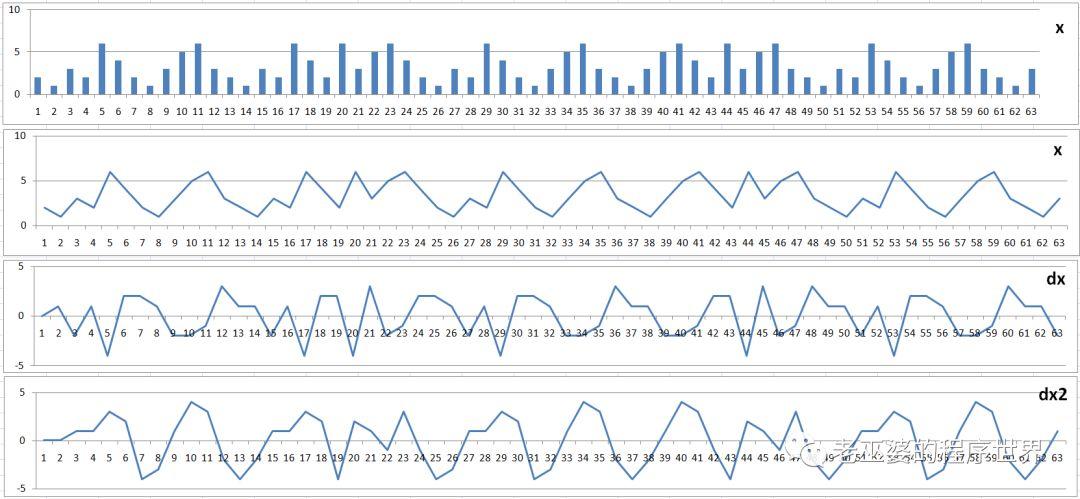
图43 对移动过程数字化后绘制的图形
图43中标题为x的两个图形是原始数据所呈现出的样子,分别为柱状图与折线图;标题为dx的图形是对原始数据进行的微分运算后的数据,即,用后项-前项的差作为绘图数据,而dx2则是二阶微分的结果(用dx的数据再进行后项-前项的运算得出)。在归纳总结过程中,试图用这些方法发现其中蕴含的规律,但是并不成功,微分后的数据与原始数据一样,并没有呈现出某种可重复的规律性,这就意味着无法使用循环语句来处理这个问题。
另一种尝试如图44所示,这是5个数字的移动顺序,将三次移动合成一组移动,并在起点(a)与终点(c)之间插入缓冲区(b),观察移动路径的变化规律。
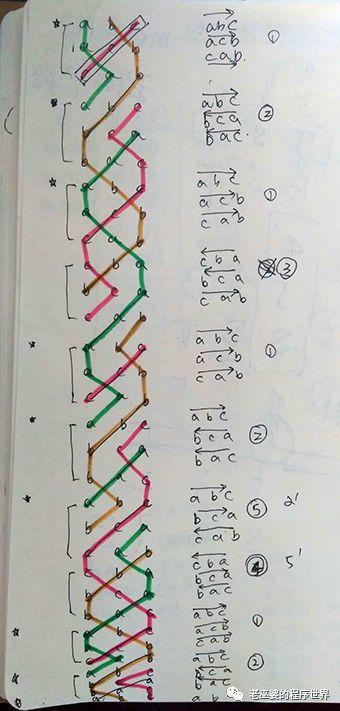
图44 在移动的起点与终点之间插入作为缓冲区的参数
上面的这些尝试虽然不总能奏效,但这样的探索过程或许具有某种启发性,因此特将这些稚拙之举拿出来与大家分享,也为自己的思索过程留下一丝痕迹。
另有几份解决问题的心得也愿与大家分享:
- 时间是不可跨越的,从起点的种子到终点的果实,思考需要一个熟化的过程;
- 重视塔高为1、2这两种情况,其实规则就蕴含在这两种情况之中,然后再用3加以验证;
- 在思考有了结果之后,再动手写代码,否则会陷在细节中而忽略了大局。
本文到此结束。

