码丁实验室,一站式儿童编程学习产品,寻地方代理合作共赢,微信联系:leon121393608。
【题目描述】
公元2044年,人类将进入宇宙纪元。$L$国有$n$个星球,分别编号为$1$到$n$,每一星球上有一个球长。因为历史的长期积淀,第i个星球上还有一位编号为i的德高望重的长者,因为长者德高望重,所以第$i$个星球的球长一定被第i位长者管辖且长者管辖自己。每一位长者手里有一份名单$B_i$,上面记录着一些长者的编号。因为一些奥妙重重的原因,第$i$位长者的名单上只可能有$1$至$i-1$中的一些编号并且保证不会重复。因为长者都德高望重,所以第$i$位长者管辖第$j$位长者的充要条件是:对于每一个$k$属于$B_i$,第$k$位长者管辖第$j$位长者。
此时,有一位记者想对一些球长进行采访,为了保证采访顺利,他决定先与一些长者搞好关系,以便采访被这些长者管辖的球长。为了与更多的球长谈笑风生,这位记者会给你提出$m$个询问。第$i$个询问中记者会给你$f_i$个长者的编号,你需要回答有多少个星球的球长至少直接或间接被一位长者管辖。≤2000000$ 。
【输入】
第一行一个数$n$,表示星球的个数。
接下来$n$行,每一行描述一个$B_i$:首先给出$B_i$的大小$sz_i$(可能为$0$),接下来$sz_i$个数,描述$B_i$中的每一个元素。保证$B_i$中的数没有重复。
接下来一行,给出一个数$m$,表示询问的个数。
接下来$m$行,每一行描述一个询问:格式同上文对于集合$B_i$的格式。
【输出】
共m行,第i行输出第i次询问的答案。
【输入样例】
7 0 1 1 1 1 1 2 2 2 3 0 2 2 6 3 2 2 3 2 3 5 2 4 5
【输出样例】
3 3 4
【提示】
【样例解释】
对于第一个询问,$2、3$号长者都管辖$1$号长者,所以总共有$3$个球长可以被采访,编号分别为$1,2,3$。
对于第二个询问,$3、5$号长者都管辖$1$号长者,所以总共有$3$个球长可以被采访,编号分别为$1,3,5$。
对于第三个询问,$4$号长者管辖第$1、2$号长者,所以总共有$4$个球长可以被采访,编号分别为$1,2,4,5$。
特别说明:第$5$号长者没有管辖长者$2$,因为$3∈B_5$但$2$不属于$B_3$。但长者$4$管辖长者$2$,因为长者管辖自己。
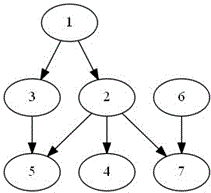 |
说明: 图中省略了球长,编号代表长者 有向边$u→v$表示$u$在$B_v$中 |
【数据规模及约定】
对于30%的数据,$n,m≤100$。
对于100%的数据,$n,m≤200000,sum|B_i|≤2000000$ ,询问中的$sum sz_i≤2000000$ 。

