友情提示：380元/半年，儿童学编程，就上码丁实验室。
【题目描述】
凯凯的工厂正在有条不紊地生产一种神奇的零件，神奇的零件的生产过程自然也很
神奇。工厂里有 $n$ 位工人，工人们从 $1 ∼ n$ 编号。某些工人之间存在双向的零件传送带。保证每两名工人之间最多只存在一条传送带。
如果 $x$ 号工人想生产一个被加工到第 $L(L > 1)$ 阶段的零件，则所有与 $x$ 号工人有传送带直接相连的工人，都需要生产一个被加工到第 $L − 1$ 阶段的零件（但 $x$ 号工人自己无需生产第 $L − 1$ 阶段的零件）。
如果 $x$ 号工人想生产一个被加工到第 $1$ 阶段的零件，则所有与 $x$ 号工人有传送带直接相连的工人，都需要为 $x$ 号工人提供一个原材料。
轩轩是 $1$ 号工人。现在给出 $q$ 张工单，第 $i$ 张工单表示编号为 $a_i$ 的工人想生产一个第 $L_i$ 阶段的零件。轩轩想知道对于每张工单，他是否需要给别人提供原材料。他知道聪明的你一定可以帮他计算出来！
【输入】
第一行两个正整数 $n$, $m$ 和 $q$，分别表示工人的数目、传送带的数目和工单的数目。
接下来 $m$ 行，每行两个正整数 $u$ 和 $v$，表示编号为 $u$ 和 $v$ 的工人之间存在一条零件传输带。保证 $u ≠ v$。
接下来 $q$ 行，每行两个正整数 $a$ 和 $L$，表示编号为 $a$ 的工人想生产一个第 $L$ 阶段的零件。
【输出】
共 $q$ 行，每行一个字符串 “Yes” 或者 “No”。如果按照第 $i$ 张工单生产，需要编号为$1$ 的轩轩提供原材料，则在第 $i$ 行输出 “Yes”；否则在第 $i$ 行输出 “No”。注意输出不含引号。
【输入样例】
3 2 6 1 2 2 3 1 1 2 1 3 1 1 2 2 2 3 2
【输出样例】
No Yes No Yes No Yes
【提示】
【输入输出样例 1 说明】
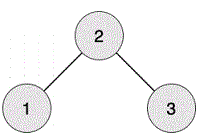
编号为 1 的工人想生产第 1 阶段的零件，需要编号为 2 的工人提供原材料。
编号为 2 的工人想生产第 1 阶段的零件，需要编号为 1 和 3 的工人提供原材料。
编号为 3 的工人想生产第 1 阶段的零件，需要编号为 2 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件，需要编号为 2 的工人生产第 1 阶段的零件，需要编号为 1 和 3 的工人提供原材料。
编号为 2 的工人想生产第 2 阶段的零件，需要编号为 1 和 3 的工人生产第 1 阶段的零件，他/她们都需要编号为 2 的工人提供原材料。
编号为 3 的工人想生产第 2 阶段的零件，需要编号为 2 的工人生产第 1 阶段的零件，需要编号为 1 和 3 的工人提供原材料。
【输入样例 2】
5 5 5 1 2 2 3 3 4 4 5 1 5 1 1 1 2 1 3 1 4 1 5
【输出样例 2】
No Yes No Yes Yes
【输入输出样例 2 说明】
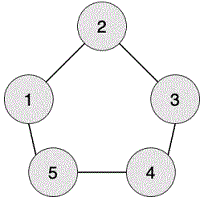
编号为 1 的工人想生产第 1 阶段的零件，需要编号为 2 和 5 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件，需要编号为 2 和 5 的工人生产第 1 阶段的零件，需要编号为 1,3,4 的工人提供原材料。
编号为 1 的工人想生产第 3 阶段的零件，需要编号为 2 和 5 的工人生产第 2 阶段的零件，需要编号为 1,3,4 的工人生产第 1 阶段的零件，需要编号为 2,3,4,5 的工人提供原材料。
编号为 1 的工人想生产第 4 阶段的零件，需要编号为 2 和 5 的工人生产第 3 阶段的零件，需要编号为 1,3,4 的工人生产第 2 阶段的零件，需要编号为 2,3,4,5 的工人生产第 1 阶段的零件，需要全部工人提供原材料。
编号为 1 的工人想生产第 5 阶段的零件，需要编号为 2 和 5 的工人生产第 4 阶段的零件，需要编号为 1,3,4 的工人生产第 3 阶段的零件，需要编号为 2,3,4,5 的工人生产第 2 阶段的零件，需要全部工人生产第 1 阶段的零件，需要全部工人提供原材料。
【数据规模与约定】
共 20 个测试点。
$1 ≤ u, v, a ≤ n$。
测试点 1~4，$1 ≤ n, m ≤ 1000，q = 3，L = 1$。
测试点 5~8，$1 ≤ n, m ≤ 1000，q = 3，1 ≤ L ≤ 10$。
测试点 9~12，$1 ≤ n, m, L ≤ 1000，1 ≤ q ≤ 100$。
测试点 13~16，$1 ≤ n, m, L ≤ 1000，1 ≤ q ≤ 10^5$。
测试点 17~20，$1 ≤ n, m, q ≤ 10^5，1 ≤ L ≤ 10^9$。