码丁实验室,一站式儿童编程学习产品,寻地方代理合作共赢,微信联系:leon121393608。
【题目描述】
给定一个 $N$ 个结点的二叉树,每个结点有个点权$F_i$,点权互不相同。
再给定$M$种交换方式,每种交换方式形如($u_i,v_i$),表示一次操作可以选择$M$种交换方式的任意一种,将$u_i,v_i$的点权交换。
求最少多少次交换,可以将原二叉树变为一个满足大根堆性质的二叉树(父亲的点权是以它为根的子树中最大的)。
【输入】
第一行,两个整数 $N$, $M$。
第二行,$N$个整数 $R_1, R_2,…, R_N$,由空格隔开。$R_i$表示点$i$的父亲。
对于二叉树的根,$R_i$用$0$表示。
第三行,$N$个互不相同的整数$F_1, F_2,…, F_N$,由空格隔开。其中 $F_i$表示点$i$的点权。
接下来$M$行,每行两个整数$u_i,v_i$,表示每种交换方式。
【输出】
仅一行,一个整数,表示总交换次数的最小值。
【输入样例】
4 4 0 1 2 3 1 2 3 4 1 2 1 4 2 3 1 3
【输出样例】
2
【提示】
【样例输入2】
5 4 3 3 5 5 0 4 8 10 9 3 1 2 2 4 1 3 4 5
【样例输出2】
6
【样例解释】
第一组样例,如下图所示。

最优方案为进行($2,3$),($1,4$)两次交换
第二组样例,如下图所示。
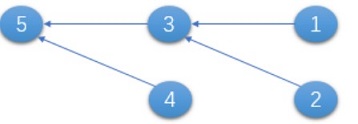
最优方案为依次进行$(1,2),(1,3),(1,2),(2,4),(2,5),(2,4)$共六次交换。
【数据规模与约定】
本题一共有10 个测试点。
下表是每个测试点的数据规模和约定:
| 测试点编号 | N= | M= | 备注 |
| 1 | 5 | 5 | 无其他限制 |
| 2 | 7 | 6 | |
| 3 | 8 | 10 | 无其他限制 |
| 4 | 9 | 30 | |
| 5 | 10 | 19 | |
| 6 | 13 | 13 | |
| 7 | 16 | 120 | |
| 8 | 10 | 12 | 答案不超过10 |
| 9 | 11 | 17 | |
| 10 | 12 | 20 |
对于100%的数据,$1≤F_i≤100$。
输入数据保证形成一个二叉树,任何两个点之间至多有一种交换方式,且交换方式不会出现自环。数据保证有解。

