码丁实验室,一站式儿童编程学习产品,寻地方代理合作共赢,微信联系:leon121393608。
【题目描述】
已知某国一共有$n$个城市,并且$1$号城市是首都。$(n-1)$条双向的公路连接这些城市,通过这些公路,任意两个城市之间存在且仅存在一条路径。每条公路有一个长度。如果一个城市只与一条公路相连,则称它为边境城市。该国政府有一个奇怪的规定:每个城市有一个封闭系数$d_i$,定义$d_i$为离这个城市最远的边境城市到这个城市的距离。市民们认为,一个城市的安全系数$S_i$和它的封闭系数有很重要的联系。$a,b,c$ 是该国的幸运数字,所以大家公认一个城市的安全系数$S_i = (d_i + a) × b bmod c$。
市民们一共会提出$m$次询问。每个询问包含三个信息,$x_i,y_i$和$q_i$。$x_i$是询问者所在的城市编号。你要为这个询问者在$x_i$到$y_i$的必经之路上找出一个离$x_i$最近的避难城市,并且要求这个避难城市的安全系数大于等于$q_i$。如果存在这样的城市(包含$x_i$和$y_i$),则输出城市编号,否则输出一行$-1$。
【输入】
第一行五个数:依次是$n, m, a, b, c$。接下来$n-1$行描述公路的信息。每行三个数,前两个数代表这条公路连接的两个城市的编号,第三个数表示这条公路的长度。再接下来$m$ 行,每行描述一个询问,包含三个数$x_i, y_i$和$q_i$。
【输出】
对于每个询问,输出一行包含一个整数,存在符合要求的城市则输出城市编号,不存在则输出$-1$。
【输入样例】
7 6 5 6 20 1 2 4 2 4 2 2 5 3 1 3 5 3 6 6 6 7 7 7 5 15 3 4 5 5 4 2 4 5 2 6 6 10 3 5 19
【输出样例】
6 3 2 4 6 -1
【提示】
【样例解释】
从城市$1$到城市 $7$ 的安全系数依次是:$18, 2, 8, 14, 0, 18, 0$。
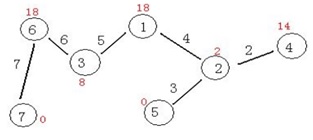
【数据规模及提示】
对于100%的数据,$0<x_i,y_i≤n$;$a,b,c,q_i≤1,000,000$。
| 测试点编号 | 范围 | 备注 |
| $1sim 5$ | $n,m≤100$ | $a,b,c<10000$ |
| $6sim 7$ | $n,m≤1000$ | |
| $8sim 10$ | $n≤100,000,m≤100$ | |
| $11sim 12$ | $n≤100,000,m≤10,000$ | 无 |
| $13sim 15$ | $n≤100,000,m≤100,000$ | 所有$y_i$相等 |
| $16sim 20$ | $n≤100,000,m≤300,000$ | 无 |
注意:计算安全系数的中间过程可能需要使用$64$位整数。

