友情提示：380元/半年，儿童学编程，就上码丁实验室。
【题目描述】
定义$fibonacci$数列第$i$项为$Fib(i)$，对于任意的大于等于$3$的$i$，有$Fib(i)=Fib(i-1)+Fib(i-2)$，令$Fib(1)=Fib(2)=1$。
再给出一个有根树$T$，$T$一共有$n$个节点，从$1sim n$编号，$1$号节点为根，每个点有一个权值，初始的时候都是$0$，现在有$2$种操作：
U X k
更新操作，对于在$X$的子树中的每一个节点(包括$X$)，如果它到$X$的距离(即这个点到$X$的唯一简单路径上经过的边数)为$D$，那么将它的权值加上$Fib(k+D)$。
Q X Y
询问操作，询问$X$到$Y$的简单路径上的所有点的权值之和(包括$X$和$Y$)，将所求的权值和$lmod 10^9+7$之后输出。
【输入】
第$1$行两个用空格隔开的正整数$n,m$表示节点个数和操作个数。
第$2sim n$行，第$i$行一个数$x$，表示节点$i$在树上的父亲是$x$。
接下来$m$行，每行一个形如”U X k“或”Q X Y“的操作。
【输出】
对于每一个询问操作，输出一行为对应顺序的询问操作的答案。
【输入样例】
5 10 1 1 2 2 Q 1 5 U 1 1 Q 1 1 Q 1 2 Q 1 3 Q 1 4 Q 1 5 U 2 2 Q 2 3 Q 4 5
【输出样例】
0 1 2 2 4 4 4 10
【提示】
【样例解释】
这是前$2$个更新操作的情况：
 |
⇒ |  |
⇒ |  |
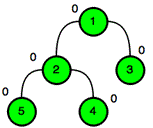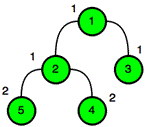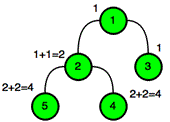【数据规模】
对于30%的数据：$n,m≤1000,k≤100$；
对于另外30%的数据：每个节点的父亲是在编号小于它的节点中随机产生的；
对于100%的数据：$n,m≤10^5$，$1≤X,Y≤n，k≤10^{15}$。