友情提示：380元/半年，儿童学编程，就上码丁实验室。
【题目描述】
组合数$C_n^m$表示的是从$n$个物品中选出$m$个物品的方案数。举一个例子，从$(1,2,3)$三个物品中选择两个物品可以有$(1,2),(1,3),(2,3)$这三种选择方法。根据组合数的定义，我们可以给出组合数$C_n^m$的一般公式：
$C_n^m=frac{n!}{m!(n-m)}$
其中$n!=1×2×…×n$。
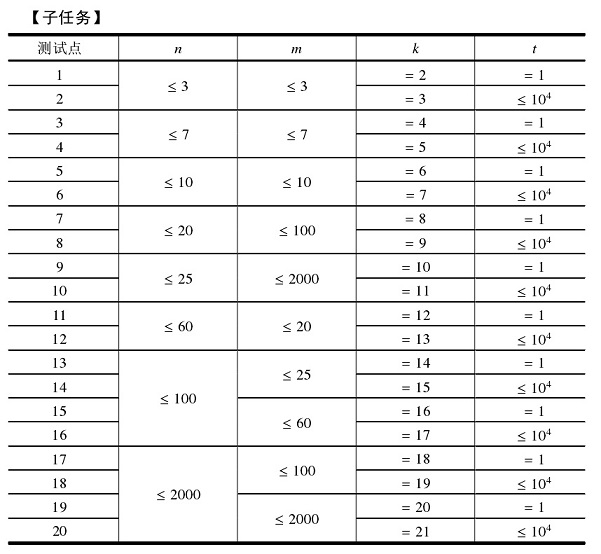
小葱想知道如果给定$n,m$和$k$，对于所有的$0≤i≤n,0≤j≤min(i,m)$有多少对($i,j$)满足$c_i^j$是$k$的倍数。
【输入】
第一行有两个整数$t, k$，其中$t$代表该测试点总共有多少组测试数据，$k$的意义见【问题描述】。
接下来$t$行每行两个整数$n, m$，其中$n, m$的意义见【问题描述】。
【输出】
$t$行，每行一个整数代表所有的$0≤i≤n,0≤j≤min(i,m)$中有多少对($i, j$)满足$C(j,i)$是$k$的倍数。
【输入样例】
1 2 3 3
【输出样例】
1
【提示】
【提示】
在所有可能的情况中，只有$C(1,2)$是$2$的倍数。
【样例2输入】
2 5 4 5 6 7
【样例2输出】
0 7
