友情提示：380元/半年，儿童学编程，就上码丁实验室。
【题目描述】
现有一块大奶酪，它的高度为 $h$，它的长度和宽度我们可以认为是无限大的，奶酪中间有许多半径相同的球形空洞。我们可以在这块奶酪中建立空间坐标系， 在坐标系中，奶酪的下表面为 $z=0$，奶酪的上表面为 $z=h$。
现在， 奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐标。如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个空洞，特别 地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞； 如果一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。
位于奶酪下表面的 Jerry 想知道，在不破坏奶酪的情况下，能否利用已有的空洞跑到奶酪的上表面去?
空间内两点 $P_1(x_1,y_1,z_1)、P_2(x_2,y_2,z_2)$ 的距离公式如下：
$dist(P_1,P_2)=(x_1−x_2)^2+(y_1−y_2)^2+(z_1−z_2)^2$
【输入】
每个输入包含多组数据。
输入的第一行，包含一个正整数 $T$，代表该输入文件中所含的数据组数。
接下来是 $T$ 组数据，每组数据的格式如下：
第一行包含三个正整数 $n,h$ 和 $r$，两个数之间以一个空格分开，分别代表奶酪中空洞的数量，奶酪的高度和空洞的半径。
接下来的 $n$ 行，每行包含三个整数 $x,y,z$，两个数之间以一个空格分开，表示空洞球心坐标为 ($x,y,z$)。
【输出】
输出包含 $T$ 行，分别对应 $T$ 组数据的答案，如果在第 $i$ 组数据中， Jerry 能从下表面跑到上表面，则输出“$Yes$”，如果不能，则输出“$No$”（均不包含引号）。
【输入样例】
3 2 4 1 0 0 1 0 0 3 2 5 1 0 0 1 0 0 4 2 5 2 0 0 2 2 0 4
【输出样例】
Yes No Yes
【提示】
样例说明：
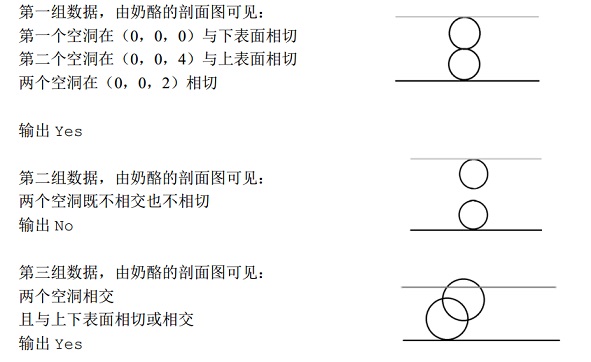
对于 20%的数据，$n=1，1≤h,r≤10,000$，坐标的绝对值不超过 $10,000$。
对于 40%的数据，$1≤n≤8，1≤h,r≤10,000$，坐标的绝对值不超过 $10,000$。
对于 80%的数据，$1≤n≤1,000，1≤h,r≤10,000$，坐标的绝对值不超过 $10,000$。
对于 100%的数据，$1≤n≤1,000，1≤h,r≤1,000,000,000，T≤20$，坐标的绝对值不超过 $1,000,000,000$。