友情提示：380元/半年，儿童学编程，就上码丁实验室。
【题目描述】
太平王世子事件后，陆小凤成了皇上特聘的御前一品侍卫。
皇宫以午门为起点，直到后宫嫔妃们的寝宫，呈一棵树的形状，某些宫殿间可以互相望见。大内保卫森严，三步一岗，五步一哨，每个宫殿都要有人全天候看守，在不同的宫殿安排看守所需的费用不同。
可是陆小凤手上的经费不足，无论如何也没法在每个宫殿都安置留守侍卫。
帮助陆小凤布置侍卫，在看守全部宫殿的前提下，使得花费的经费最少。
【输入】
输入中数据描述一棵树，描述如下：
第一行 $n$，表示树中结点的数目。
第二行至第 $n+1$ 行，每行描述每个宫殿结点信息，依次为：该宫殿结点标号 $i(0 < i≤n)$，在该宫殿安置侍卫所需的经费 $k$，该边的儿子数 $m$，接下来 $m$ 个数，分别是这个节点的 $m$ 个儿子的标号$r_1,r_2,cdots ,r_m$ 。
对于一个 $n$ 个结点的树，结点标号在 $1$ 到 $n$ 之间，且标号不重复。
【输出】
输出最少的经费
【输入样例】
6 1 30 3 2 3 4 2 16 2 5 6 3 5 0 4 4 0 5 11 0 6 5 0
【输出样例】
25
【提示】
样例解释：
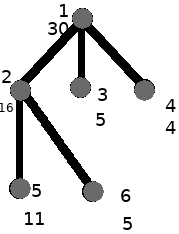
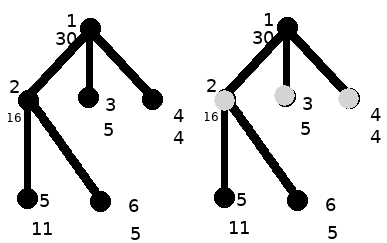
有六个区域被安排的情况如左图所示。
如右图，灰色点安排了警卫，$2$ 号警卫可以观察 $1,2,5,6$，$3$ 号警卫可以观察 $1,3$，$4$ 号警卫可以观察 $1,4$。
总费用：$16+5+4=25$
数据范围与提示：
对于 100% 的数据，$0<n≤1500$。